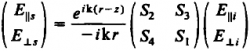Здесь находится вводное описание метода Finite-Difference Time-Domain (FDTD).
FDTD (Finite-Difference Time-Domain)
FDTD является одним из наиболее популярных методов для численного решения уравнений Максвелла. Базовый алгоритм этого метода был предложен Кейном Йи в 1966 г. Однако имеющуюся популярность FDTD приобрел только в 90х гг. прошлого столетия, когда он стал основным для моделирования самых разных оптических приложений. Вот некоторые причины его популярности:
- Присущая методу высокая параллельная эффективность позволяет проводить расчеты больших задач на кластерных вычислительных системах;
- FDTD удобен при задании сложных геометрических объектов, а также анизотропных, дисперсных и нелинейных сред;
- В FDTD существует возможность как для анализа зависимости свойств оптических объектов от длины волны, так и для моделирования нестационарных процессов;
- FDTD предоставляет возможность наблюдать реальное поведение полей во времени.
В первоначальном узком смысле под FDTD подразумевалось использование базового алгоритма Йи для численного решения уравнений Максвелла. В современном более широком смысле FDTD включает в себя множество самых разнообразных возможностей: моделирование сред с дисперсными и нелинейными свойствами, применение различных типов сеток (помимо первично предложенной прямоугольной сетки Йи), использование методов постпроцессорной обработки результатов и т. д.
Для реализации указанных возможностей требуется написание больших параллельных программ. Имеются коммерческие решения, однако они не могут удовлетворить исследователей, которые хотели бы понимать, как работает программа, а не иметь дело с черным ящиком. Это явилось причиной разработки открытой библиотеки EMTL (Electromagnetic Template Library).
Алгоритм Йи
Алгоритм Йи представляет собой простую и элегантную схему дискретизации уравнений Максвелла, записанных в дифференциальной форме. Сетки для электрического и магнитного полей смещены по отношению друг к другу на половину шага дискретизации по каждой из пространственных переменных и по времени. Конечно-разностные уравнения позволяют определить электрические и магнитные поля на данном временном шаге на основании известных значений полей на предыдущем, и при заданных начальных условиях вычислительная процедура дает эволюционное решение во времени от начала отсчета с заданным временным шагом.
В отсутствие свободных зарядов уравнения Максвелла в дифференциальной форме имеют вид:
где и
- напряженности электрического и магнитного полей,
- электрическая,
- магнитная индукция,
- плотность электрического тока,
- ее магнитный аналог, который мы включили для общности некоторых используемых далее выражений.
В целях простоты изложения мы ограничим рассмотрение только изотропными, недисперсными и линейными среды. Тогда вектора и
,
и
связаны следующими соотношениями:
где ,
,
,
- абсолютные и относительные диэлектрическая и магнитная проницаемости среды,
и
- электрическая и магнитная постоянные.
Плотность электрического и магнитного токов представим в виде:
где - плотность тока свободных источников,
- электропроводность,
и
- их магнитные аналоги.
Подставив эти соотношения в первую пару уравнений Максвелла, получим
Согласно алгоритму Йи, уравнения Максвелла дискретизуются с использованием центрального разностного отношения для приближения пространственной и временной производных. Для этого сеточные узлы, в которых хранятся компоненты электрического и магнитного полей, смещены по отношению друг к другу на половину сеточного шага по каждой из пространственных переменных. В результате те узлы, которые соответствуют компонентам полей расположены таким образом, что каждая компонента
окружена четырьмя компонентами
, и наоборот.
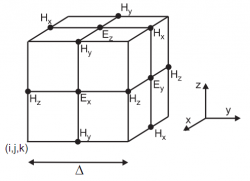
Положения сеточных узлов для компонент электрического и магнитного полей на сетке Йи.
Согласно алгоритму Йи соответствующие компонентам и
узлы сдвинуты относительно друг друга по времени на половину временного шага (в качестве примера это продемонстрировано ниже для одномерной сетки Йи). Для расчета значений поля
на
-ом временном шаге используются значения поля
на
-ом. Аналогичным образом значения поля
на
-ом шаге рассчитываются с использованием значений поля
на
-ом шаге. Эта процедура продолжается до тех пор, пока расчет не будет закончен.
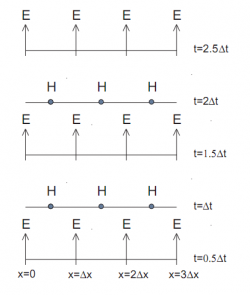
Развертка одномерной сетки Йи по времени: узлы, соответствующие электрическому и магнитному полям, сдвинуты друг относительно по пространству и по времени на половину шага.
Прежде чем получить конкретные разностные уравнения, используемые в алгоритме Йи, введем следующие обозначения. Будем ставить в соответствие каждому сеточному узлу три целых числа ,
и
, определяющих положение этого узла в пространстве как
где
,
и
суть сеточные шаги по соответствующим направлениям. Будем обозначать произвольную сеточную функцию
как
где - шаг по времени, а
- текущий временной шаг.
Как уже упоминалось, в алгоритме Йи для аппроксимации присутствующих в уравнениях Максвелла производных используется центральное разностное отношение. Так, для производной по координате в точке
в момент времени
имеем
Аналогично для производной по времени
Применяя эти приближения для производных, участвующих в проекции закона Ампера на ось
получаем
Стоящие в правой части переменные берутся на временном шаге , включая поле
. Поскольку для значения
в момент времени
данных на сетке нет, нужно для него пользоваться каким-либо приближением. Хорошим выбором является усреднение по соседним временным слоям:
Положим . Тогда мы можем явно выразить
на
шагу:
где
Мы получили разностное уравнение, соответствующее проекции закона Ампера на ось , которое вместе с пятью оставшимися аналогичными разностными уравнениями и формируют алгоритм Йи.
Можно показать, что в случае непроводящей среды () и при отсутствии источников тока
два оставшиеся незадействованными нами уравнения Максвелла выполняются автоматически, а именно, дивергенция полей
и
всегда равна нулю. При наличии источников тока справедливость двух оставшихся уравнений не вытекает непосредственно из разностной схемы, но с хорошей точностью подтверждается в численном эксперименте.
Выбор значений ,
,
обуславливается геометрией задачи и спектральным составом излучения. Можно дать следующую рекомендацию: на характерный размер объекта (радиус шариков, толщину экрана и т. п.) должно приходится не менее нескольких сеточных шагов, а на характерную длину волны - от десяти и больше. Величина значения
ограничена сверху условием Куранта
выполнение которого необходимо для устойчивости разностной схемы.
В этом параграфе мы рассмотрели реализацию алгоритма Йи для случая, когда среда характеризуется не зависящими от частоты скалярными значениями ,
,
,
. Численное моделирование анизотропных, дисперсных и нелинейных сред требует модификации этого алгоритма и применения вспомогательных разностных уравнений.
Отметим также, что численная схема FDTD не предполагает возможности табличного задания зависимости диэлектрической проницаемости от частоты. Как моделировать в FDTD дисперсные материалы, можно прочитать в разделе Фитинг диэлектрической проницаемости.
Численный эксперимент FDTD
Перечислим «основных участников» численного эксперимента FDTD.
- Материальные тела, оптические свойства которых мы исследуем.
- Источник электромагнитной волны. Самый простой способ задания источника заключается в задании временной зависимости величины
в уравнениях Максвелла. Такой тип источника обычно используется при моделировании диполей. Для генерации плоской волны более удобен другой тип источника, реализуемый с помощью метода полного и рассеянного поля (total field / scattered field method).
- Детекторы, снимающие поля на сетке в течение всего численного эксперимента. Детекторам не отвечают какие-то реальные тела в пространстве, под ними подразумевается лишь то, что мы записываем значения полей в каких-то точках внутри вычислительного объема в файл. По окончании расчета на основании этого файла можно будет восстановить ход численного эксперимента. Детекторы могут размещаться в произвольном месте вычислительного объема и не привязаны к сетке. Значения полей на них получаются путем интерполяции по соседним сеточным узлам.
Обычный сценарий численного эксперимента FDTD выглядит так:
- Внутри вычислительного объема, задаваемого размером используемой сетки, помещаются материальные тела, источник и детекторы (детекторам не отвечают какие-то реальные тела в пространстве, под ними подразумевается лишь то, что мы записываем значения полей в каких-то точках в файл). На границе вычислительного объема должны быть заданы граничные условия, обычно, периодические или поглощающие.
- Источник генерирует конечную во времени электромагнитную волну, спектральный состав которой должен покрывать интересующий нас диапазон частот. Далее, волна падает на тела, перерассеивается на них, и, при наличии поглощающих граничных условий, через какое-то время уходит из вычислительного объема. История распространения волны фиксируется детекторами.
- С помощью преобразования Фурье записанные на детекторах значения полей переводятся в частотное представление. Далее, обрабатывая их (например, интегрируя поток энергии поля через какую-либо поверхность), мы получаем интересующие нас оптические характеристики рассматриваемой структуры тел.
Поясним некоторые использованные нами понятия.
Метод полного и рассеянного поля
Этот метод используется для моделирования бесконечно удаленного источника плоской волны. Этот метод основан на линейности уравнений Максвелла и вытекающего из них принципа суперпозиции. А именно, мы предполагаем, что измеряемое (полное) поле и
может быть представлено в виде суммы
,
соотвествует полю падающей волны, которая предполагается известной во всех точках пространства в любой момент времени. Это та волна, которая распространялась бы в пространстве, если бы в нем не существовало никаких тел.
,
соответствует рассеянной волне, представляющей собой результат взаимодействия падающей волны с телами. Значение рассеянной волны заранее неизвестно.
Разностные уравнения FDTD могут независимо применяться как для полного поля, так и для падающего или рассеянного полей. Это позволяет разбить вычислительный объем на две области: область полного поля, в которой рассчитывается полное поле, и область рассеянного поля, в которой рассчитывается рассеянное поле. Эти две области разделяет виртуальная граница, которая служит для генерации плоской волны в область полного поля. Разностные уравнения, используемые для расчета компонент поля в прилегающих к этой границе сеточных узлах, отличаются от исходных наличием дополнительных слагаемых, в которых учитывается значение поля падающей волны.
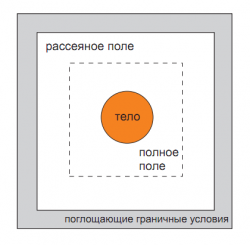
Схема численного эксперимента FDTD с использованием метода полного и рассеянного поля.
Поглощающие граничные условия
Для устранения нефизичного переотражения электромагнитной волны от границы вычислительного объема и моделирования таким образом ухода волны на бесконечность в FDTD должны использоваться особые поглощающие граничные условия. В настоящее время наиболее успешной реализацией этих условий является помещение вдоль границы вычислительного объема тонкого слоя специального материала, называемого идеально согласованным слоем (Perfectly Matched Layer - PML). Этот материал в идеале полностью поглощает все падающие на него волны без какого-либо отражения независимо от угла падения и длины волны.
Понятие идеально согласованного слоя (PML) было введено Дж.-П. Беренгером в 1994 году. Работа такого слоя основывалась на разбиении исходных полей и
на две компоненты, для каждой из которых должны решаться свои уравнения. Впоследствии были предложены усовершенствованные формулировки PML эквивалентные первоначальной формулировке Беренгера. Так, в одноосном PML (Uniaxial PML) используется анизотропный поглощающий материал, что позволяет не вводить дополнительные переменные и остаться в рамках исходных уравнений Максвелла. Однако одноосный PML, как и PML в формулировке Беренгера, не удобны тем, что в них отсутствует поглощение затухающих волн, что не позволяет помещать PML близко к рассеивающим телам. Этого недостатка лишен оборотный PML (Convolutional PML), основанный на аналитическом продолжении уравнений Максвелла в комплексную плоскость таким образом, что их решение экспоненциально затухает. CPML также удобнее в ограничении бесконечных проводящих и дисперсных сред. Помимо этого математическая формулировка CPML обладает большей наглядностью и доступностью для понимания.
В некоторых случаях использование PML приводит к расходимости FDTD. Эту проблему можно устранить путем использования Additional back absorbing layers technique httpPDF
Периодические граничные условия
FDTD может применяться не только для конечных, но и для бесконечных периодических структур. Для их моделирования используются периодические граничные условия по одному или по нескольким направлениям. В частности, фотонно-кристаллические пластинки и антиотражающие покрытия являются планарными периодическими структурами: они периодичны по двум направлениям и имеют ограниченную протяженность по оставшемуся направлению. Реальные экспериментальные образцы, конечно, имеют ограниченный размер и по первым двум направлениям, но поскольку этот размер существенно больше их протяженности по непериодическому направлению, влиянием конечности образца с хорошей степенью точности можно пренебречь.
В практических приложениях, как правило, наиболее интересны спектры прохождения и отражения от рассматриваемых структур. Для их получения в случае нормального падения в FDTD используется следующий численный эксперимент. Граница между областями полного и рассеянного поля генерирует плоскую волну в форме ограниченного по времени импульса, который падает на структуру (на рисунке ниже этот импульс генерируется на границе 1 и движется слева направо). Часть падающего импульса отражается от структуры, пересекает плоскость, в которой находятся детекторы, меряющие отраженную волну (плоскость 2 на рисунке), и поглощается задним слоем PML. Другая часть проходит сквозь структуру, пересекает плоскость, в которой расположены детекторы, меряющие прошедшую волну (плоскость 2' на рисунке), и поглощается передним слоем PML. Численный эксперимент продолжается до тех пор, пока сигнал не выйдет из вычислительного объема. Время выхода сигнала зависит от конкретной геометрии эксперимента. При увеличении продольной протяженности структуры это время увеличивается по причине увеличения расстояния, которое должен пройти сигнал, чтобы из нее выйти. Время выхода сигнала зависит также и от оптических свойств исследуемой структуры, например, при наличии поглощения оно меньше.
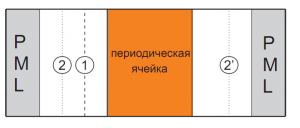
Схема численного эксперимента FDTD для расчета спектров прохождения и отражения планарной периодической структуры в случае нормально падения. 1 – генерирующая электромагнитный импульс граница между областями полного (справа от 1) и рассеянного (слева от 1) поля; 2, 2' - плоскости, в которых расположены детекторы для измерения отраженной и прошедшей волны соответственно.
По окончании эксперимента записанные детекторами значения полей ,
переводятся в частотное представление с помощью дискретного преобразования Фурье. Далее, рассчитывая среднее значение вектора Пойнтинга по времени
на каждом из детекторов по формуле
мы можем посчитать средний поток энергии , проходящий через поверхность
, на которой расположены детекторы:
Нормируя поток энергии прошедшей и отраженной волны на падающий импульс, мы получаем интересующие нас спектры прохождения и отражения
. Поглощение вычисляется как
.
Схема FDTD для моделирования наклонного падения плоской волны на периодическую структуру может быть найдена здесь httpPDF
Метод подсеточного сглаживания
Как и в любом другом разностном методе, в FDTD существует проблема неточного отображения границы тела на вычислительную сетку. В непосредственной близости от границы двух сред уравнения Максвелла должны решаться с учетом граничных условий для векторов и
. Любая кривая поверхность, разделяющая соседние среды и геометрически не согласованная с сеткой, будет искажаться эффектом «лестничного приближения». В результате порядок точности FDTD понижается с изначального второго до первого.
Для решения данной проблемы были предложены различные методы. Первая группа методов основана на изменении способа дискретизации уравнений Максвелла с той целью, чтобы сетка максимально соответствовала рассматриваемой геометрии. Например один из таких методов заключается в увеличении разрешения сетки в тех областях пространства, где расположены тела со сложной геометрической структурой. Также можно видоизменять разностные уравнения в узлах сетки, находящихся вблизи границы между соседними телами. Более радикальным шагом является введение нерегулярной неортогональной сетки, которая полностью согласовывалась бы с рассматриваемой геометрией. Такая сетка автоматически генерируется программой, которая следит за расстановкой всех тел в пространстве. Общим недостатком упомянутых методов является увеличение объема требуемой памяти и порой существенное снижение производительности.
Другая группа методов основывается на введении эффективной диэлектрической проницаемости вблизи границы между телами. Рассмотрим некоторый контрольный объем
, окружающий выбранный узел сетки, и предположим, что он содержит границу раздела между двумя средами со значениями диэлектрической проницаемости
и
. Тогда граничные условия для векторов
могут быть реализованы на сетке путем ввода тензора обратной диэлектрической проницаемости в форме:
где - это матрица
соответствующая проектору на вектор нормали
к границе между двумя средами, а
есть усреднение по объему.
Более подробно о реализации этого метода в FDTD можно почитать здесь httpPDF
Применение FDTD
FDTD применяется в самых разнообразных приложениях: для расчета рассеяния падающей волны на различных структурах, для моделирования излучения источника в заданном электромагнитном окружении, для изучения оптических свойcтв резонаторов и волноводов. Ниже мы изложим, какие величины при этом измеряются.
Предварительные замечания
Напомним, что любое решение уравнений Максвелла (
это либо
, либо
) в случае линейных сред и при отсутствии свободных зарядов и источников тока может быть представлено в виде суперпозиции гармонических полей:
.
Удобно рассматривать вектор как действительную часть от комплексного вектора
,
где
:
.
Комплексная зависимость не несет никакого физического смысла и вводится лишь для удобства.
Вектор плотности потока электромагнитной энергии (вектор Пойнтинга) равен . В монохроматической волне его величина быстро осциллирует, чего большинство приборов отследить не в силах. Вместо этого измеряют среднее вектора Пойнтинга по времени
:
,
где временной интервал существенно больше частоты
.
Можно показать, что для монохроматической волны
.
Абсолютная величина вектора называется интенсивностью света
.
Рассеяние на теле
Рассмотрим задачу о рассеянии падающей волны на заданном теле. Поле вне тела можно представить в виде суммы падающей и отраженной волн:
.
В задаче о рассеянии интересуются количеством энергии рассеянной волны, ее угловой зависимостью, а также количеством поглощаемой телом энергии.
Окружим тело воображаемой замкнутой поверхностью . Средняя скорость, с которой энергия притекает в ограниченный ею объем, равна
,
где - нормаль к поверхности.
Если , энергия поглощается внутри объема. Если внешняя среда является непоглощающей, то
есть энергия, поглощаемая телом.
В нашем случае среднее по времени от вектора Пойнтинга может быть записано в виде суммы трех слагаемых (нижний индекс
для комплексных векторов
и
мы опускаем)
,
где каждое слагаемое по отдельности равно
.
Наличие есть следствие интерференции падающей и отраженной волн.
Учитывая только что сказанное, для получаем
,
.
В случае непоглощающей внешней среды , и
Поскольку рассматриваемые величины линейно зависит от интенсивности падающей волны , имеет смысл рассматривать отношения
,
имеющее размерность площади, и называемые сечениями экстинции, поглощения и рассеяния
Можно определить эффективности экстинции, рассеяния и поглощения
,
где - площадь проекции тела на плоскость перпендикулярную направлению падающей волны (для сферы радиуса
имеем
). На длинах волн больших размеров тела, тело может рассеивать и поглощать больше света, чем падает на его геометрическое сечение. Соответствующие эффективности при этом будут больше единцы.
Матрица амплитуд рассеяния
Помимо энергии рассеянной волны часто интересуются ее угловым распределением, которое характеризуется матрицей амплитуд рассеяния. Вводится она следующим образом.
Пусть на тело падает монохроматическая линейно поляризованная волна.
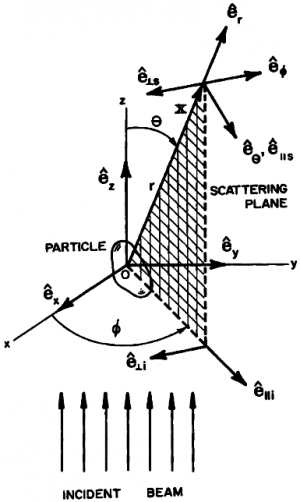
Направим ось вдоль направления падения. Выберем какую-либо точку внутри тела в качестве начала координат
, а оси
,
направим произвольно. Нашей системе координат соответствуют ортонормированный базис векторов
,
,
.
Направление рассеяния вместе с направлением падения
определяют плоскость рассеяния, которая однозначно задается азимутальным углом
, если только
не параллельно оси
. В этих двух случаях (
) любая плоскость параллельная оси
может считаться плоскостью рассеяния.
Вектор падающего электрического поля, лежащий в плоскости
, удобно разложить на две компоненты, одна из которых параллельна плоскости рассеяния, а другая перпендикулярна ей
Вектора ортонормированного базиса
,
образуют правую тройку с вектором :
Кроме того, имеем
,
где ,
,
образуют базис, связанный с полярной системой координат
.
Если компоненты падающего поля в направлениях x и y обозначить через и
, то
,
.
Известно, что на больших расстояниях от тела () (в так называемой дальней зоне) рассеянное поле приближенно является поперечным (
), и, может быть записано как
,
где
.
Базисный вектор параллелен, а
перпендикулярен плоскости рассеяния. Заметим, однако, что
и
определены в разных системах базисных векторов. Тем не менее, вследствие линейности уравнений Максвелла, связь между ними можно представить в матричном виде
где комплексные числа (
) составляют амплитудную матрицу рассеяния, зависящую от угла рассеяния
и азимута
.
Экспериментальное измерение матричных элементов затруднительно, поэтому обычно меряют элементы матрицы рассеяния, связывающей так называемые параметры Стокса для падающей и рассеянной волн. Это действительная матрица
, из 16 элементов которой независимы только семь, которые в свою очередь могут быть выписаны через абсолютные значения
и разницы в фазе между
. Желающие узнать об этом более подробно, могут ознакомиться с главой 3.3 книги 1).
Коэффициенты прохождения и отражения для плоскопериодических структур
Радиационное затухание источника
Приложения
Программа EMTL использовалась для решения различных оптических задач на многих кластерных вычислительных системах. Ниже представлен лист избранных публикаций:
Смотрите также диссертацию Алексея Дейнеги.