Учебный курс
В этом разделе на тестовых примерах иллюстрируется, как с помощью EMTL проводить численные расчеты FDTD. Подробное описание используемых для этого классов находится в разделе Документация.
Единицы измерения
У нас в программе применяется запись уравнений Максвелла без коэффициентов типа ,
,
,
. Это приводит к тому, что единицы измерения поля отличны от единиц измерения СИ, но никаких неудобств это не создает, поскольку все интересующие нас величины (такие, как коэффициент прохождения или сечение рассеяния) выражаются в виде отношения полей.
Скорость света полагается равной единице, а значит частота электромагнитной волны (например, волне с частотой 10 соответствует длина волны 0.1). Единицей измерения времени является время необходимое свету для того, чтобы пройти единицы длины.
Подключение EMTL
Подключение EMTL осуществляется с помощью заголовочного файла uiexp.h.
#include "uiexp.h"
Перед использованием библиотеки вы должны провести ее внутреннюю инициализацию с помощью функции emInit, куда передаются аргументы командной строки.
int main(int argc, char **argv){ emInit(argc,argv); ... // ваш код return 0; }
У функции emInit имеются третий и четвертый необязательные аргументы. В них можно указывать имена для директории, куда записываются текстовые выходные файлы, и для директории, куда записываются большие вспомогательные двоичные файлы. По умолчанию эти аргументы равны пустым строкам, а все файлы пишутся в ту директорию, где находится исполняемый файл.
Проведение эксперимента FDTD осуществляется посредством класса uiExperiment, объявленного в файле uiexp.h. Нужно создать объект этого класса, а далее последовательно вызывать его функции, с помощью которых задается геометрия эксперимента, проводится расчет и последующий анализ.
Геометрические тела
Как создавать геометрические тела описано здесь.
Если тела выходят за границы вычислительного объема, то рассматривается только та их часть, которая в него попадает.
Среды
Среде отвечает класс emMedium. В его конструктор передаются диэлектрическая проницаемость , электропроводность
, магнитная проницаемость
и магнитные потери
. По умолчанию их значения равны 1, 0, 1, 0.
FDTD не предполагает возможности табличного задания зависимости диэлектрической проницаемости от частоты. Однако в FDTD можно задать эту зависимость в виде произвольного числа членов в форме Друде и Лоренца:
Например, золото можно задать следующим образом
emMedium m(5.4); m.AddPolarizability(emDrude(.14*1e17,.103*1e+15/2,1)); m.AddPolarizability(emLorentz(.427*1e+16,.87*1e+15,2.54*.268)); m.AddPolarizability(emLorentz(.523*1e+16,1.32*1e+15,2.54*.732)); m.calibrate(1/(299792458*1e+6));
Параметры конструкторов для членов Друде и Лоренца такие: плазменная частота и затухание
и величина
. Конкретные данные для золота взяты отсюда.
Задаваемая плазменная частота и затухание
должны измеряться в радианах на единицу измерения времени FDTD. В данном примере изначальные данные для золота имеют размерность радиан / секунду. Если единицей измерения длины FDTD является микрон, то, соответственно, единицей измерения времени FDTD является время, за которое свет проходит один микрон. Для того, чтобы придать значениям
,
требуемую размерность, мы воспользовались функцией calibrate, которая умножает
и
(а также
и
) на свой аргумент (в данном случае на обратную скорость света, сек/мкм).
В случаях, когда у Вас имеется табличная зависимость диэлектрической проницаемости среды от частоты, ее необходимо аппроксимировать с помощью произвольного числа членов Друде, Лоренца. Для некоторых часто используемых сред (золото, серебро, кремний, вольфрам и т. д.) такая аппроксимация уже есть в файле opt_data.h. Для того, чтобы ей воспользоваться, нужно вызвать подходящую функцию, возвращающую объект emMedium, например
emMedium au=GetAu(); // au - среда, отвечающая золоту
вернет золото из предыдущего примера. В этом примере предполагается, что единица длины FDTD равна одному микрону. Если у вас единица длины FDTD равна 0.1 микрону, то нужно писать
emMedium au=GetAu(0.1);
В EMTL имеется также поддержка членов в форме Дебая, однако она сейчас недоступна.
Рассеяние на сфере
Создадим последовательно код, задающий эксперимент с рассеянием плоской волны на сфере. Задача о рассеянии на сфере имеет аналитическое решение, пользуясь которым, мы сможем удостовериться в том, что код работает правильно.
Создадим объект этого класса uiExperiment:
uiExperiment task;
Вычислительным объемом у нас будет являться параллелепипед с противоположным координатами (-10,-10,-10) и (10,10,10).
task.SetInternalSpace(Vector_3(-10),Vector_3(10));
Зададим поглощающие граничные условия PML по всем трем направлениям.
task.SetBC(BC_PML,BC_PML,BC_PML);
Шаг по сетке dr будет равен единице.
task.SetResolution(1);
Второй необязательный аргумент функции SetResolution есть отношение шага по времени к шагу по сетке, значение по умолчанию для которого равно 0.5 (при этом значении FDTD работает устойчиво). Это означает, что шаг по времени в нашем случае равен .
Теперь мы можем сразу перейти к расчету:
task.Calculate(200); task.Analyze();
Аргумент функции Calculate равен времени FDTD, в течение которого будет выполняться эксперимент. Поскольку шаг по времени равен 0.5, количество временных итераций равно .
Итак, мы получили следующий код:
#include "uiexp.h" int main(int argc, char **argv){ emInit(argc,argv); uiExperiment task; task.SetInternalSpace(Vector_3(-10),Vector_3(10)); task.SetBC(BC_PML,BC_PML,BC_PML); task.SetResolution(1); task.Calculate(200); return 0; }
После того, как мы скомпилируем и запустим его (о том, как это делается, написано в разделе «Установка»), программа выдаст сообщения, отражающие ход ее работы. Как будет из них видно, она честно выполнит свои 400 итераций (в сообщених выдается 399, потому что нумерация итераций начинается с нуля).
Как следует сообщений, размер сетки по каждому направлению равен 40 шагов. Это связано с тем, что к размеру внутреннего вычислительного объема, равного , прибавился еще задний и передний слои PML толщиной 10 шагов (10 шагов это оптимальное значение по умолчанию, которое можно менять с помощью функции ConfPML).
Поскольку начальное значение поля на сетке равнялось нулю, а источников света в нашем эксперименте нет, то конечное значение поля тоже нуль. Фактически, мы считали вакуум, в котором ничего не происходит.
Далее мы будем последовательно заполнять вычислительный объем телами, источниками и детекторами, вызывая различные функции класса uiExperiment. Создаваемый код нужно помещать перед вызовом функции Calculate.
Total Field / Scattered Field
Для генерации плоской волны мы будем используеть метод Total Field / Scattered Field (TF/SF). Область Total Field будет находится внутри параллелепипеда с координатами противоположных вершин (-7,-7,-7) и (7,7,7).
task.AddTFSFBox(Vector_3(-7),Vector_3(7));
В качестве падающей волны, используемой в области Total Field, будем использовать ограниченный по времени импульс с плоским фронтом, распространяющийся в направлении (0,0,1), и поляризованный вдоль направления (1,0,0):
task.SetPlaneWave(Vector_3(0,0,1),Vector_3(1,0,0));
Зададим временную зависимость падающего импульса в форме Беренгера:
task.SetSignal(new Berenger(1,25,5,125));
Форма Беренгера выглядит так:
,
,
В нашем примере ,
,
,
Детекторы
Для того, чтобы измерять поля внутри вычислительного объема, нужны детекторы. Они считывают значения поля в тех точках, куда они помещены, никак при этом на него не влияя. Значения на детекторах получаются путем интерполяции по близлежащим узлам сетки. В ходе численного эксперимента детекторы записывают свои показания в двоичные файлы. Далее на основании этих двоичных файлов будут созданы читаемые текстовые файлы.
Поместим наш первый детектор в центр вычислительного объема:
task.AddDetectorSet("c",Vector_3(),Vector_3(),iVector_3(1));
Первый параметр функции AddDetectorSet – имя множества детекторов, которое будет содержаться в названии соответствующих выходных файлов. Следующие три параметра задают трехмерную сетку, на которой расположены детекторы (левый нижний и правый верхний вершины сетки и количество сеточных шагов вдоль трех направлений). В нашем случае эта сетка вырождается в точку (0,0,0).
Во время работы функции Calculate детектор будет записывать свои показания в двоичный файл binary.c.dat. Для того, чтобы из этого файла сделать текстовую таблицу, нужно после вызова Calculate вызвать функцию Analyze
task.Analyze()
В результате будет создан текстовый файл c_r0000.d, в котором будет записана история поля в детекторе в виде таблицы с колонками t, x, y, z, Ex, Ey, Ez, Hx, Hy, Hz для времени, координат и значений полей E и H.
Для построения графиков на основании выходных текстовых файлов EMTL мы пользуемся популярной графической программой gnuplot, которая скачивается отсюда http://www.gnuplot.info.
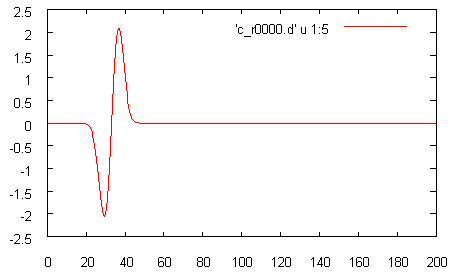
Например, для просмотра истории значения компоненты Ex во времени в файле c_r0000.d, нужно открыть гнуплот, с помощью команды cd перейти в нужную директорию (имя директории должно быть в кавычках), а потом в нем набрать
gnuplot> p 'c_r0000.d' u 1:5 w l
В результате вы увидите заданный нами импульс Беренгера.
У функции AddDetectorSet есть пятый необязательный параметр, куда можно помещать разные битовые флаги.
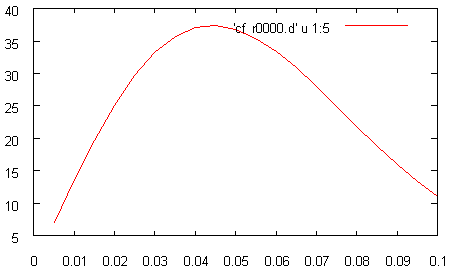
Например, для получения поля в частотном представлении нужно включить флаг DET_F:
task.AddDetectorSet("cf",Vector_3(),Vector_3(),iVector_3(1),DET_F);
В выходном текстовом файле cf_r0000.d будет представлена зависимость поля от частоты. Как видно из рисунка ниже, центральная частота нашего импульса примерно равна 0.04, что соответствует длине волны 25.
Фильм с распространением волны
Мы научились получать временную историю сигнала и частотную форму сигнала в точке. Для того, чтобы посмотреть поле во всем вычислительном объеме, можно покрыть его сеткой детекторов.
Например, создадим двумерную сетку детекторов, параллельную плоскости yz и проходящую через центр координат (0,0,0).
task.AddDetectorSet("f",Vector_3(-9.5),Vector_3(9.5),iVector_3(1,20,20),DET_TSTEP);
Отметим, что поскольку количество узлов сетки вдоль ось x равно одному, x координата узлов равна (-9.5+9.5)/2=0. Если бы количество узлов было больше одного (как для случая других двум направлений), крайние узлы сетки оказались бы в точках -9.5 и 9.5. Если вам не очень понятно, что здесь имеется в виду, имеет смысл построить разные сетки детекторов и посмотреть на них в гнуплоте (о том, как это делать, будет идти речь ниже).
По умолчанию на выходе программа создает текстовые файлы в каждом из которых находится история сигнала для определенного детектора. Для того, чтобы создать выходные файлы для каждого временного шага со значениями полей на всей сетке детекторов, нужно использовать флаг DET_TSTEP.
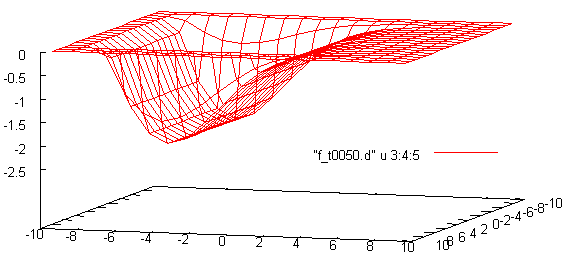
В нашем случае это приведет к созданию файлов f_txxxx.d, где xxxx – номер временной итерации. Просмотрим распределение поля на 50 временной итерации, набрав в гнуплоте:
gnuplot> sp 'f_t0050.d' u 3:4:5
Для последовательного просмотра всех итераций создадим файл film.gnu и скопируем в него следующий скрипт
pref="f"
fn=sprintf("\%s\_t\%04d.d",pref,i)
splot [][][-3:3] fn u 3:4:5 w l
i=i+1
if(i<iterations)reread
Запустим его, набрав в командной строке
gnuplot> i=0; iterations=400; load 'film.gnu'
В итоге мы увидим плоскую волну в форме импульса Беренгера, проходящую в области Total Field.
Фильм можно сделать более симпатичным, если значение поля Ex будет передаваться не высотой по оси z, а непрерывно меняющимся цветом. Для этого наберем в командной строке gnuplot
gnuplot> set pm3d interpolate 2,2 gnuplot> cbr=3 gnuplot> set palette defined (-cbr 'blue', 0 'white', cbr 'red') gnuplot> set cbrange [-cbr:cbr] gnuplot> set view 0,0
а в скрипте film.gnu вместо
splot [][][-3:3] fn u 3:4:5 w l
напишем
splot [][][-cbr:cbr] fn u 3:4:5 w pm3d
Допустим, мы хотим создать видео. Для этого наберем в командной строке
gnuplot> set terminal png
Теперь выходные данные gnuplotа будут выводиться не на экран, а в файл в формате 'png'.
Модифицируем наш скрипт следующим образом
pref="f"
fp=sprintf("\%s\%04d.png",pref,i)
set output fp
fn=sprintf("\%s\_t\%04d.d",pref,i)
splot [][][-cbr: cbr] fn u 3:4:5 w pm3d
i=i+1
if(i<iterations)reread
Запустив его, мы получим 400 картинок, которые впоследствии можно слить в один файл avi (например, программой VirtualDub).
Чтобы вернуться в режим вывода на экран и вернуться из режима pm3d, нужно набрать
gnuplot> set terminal win gnuplot> unset pm3d
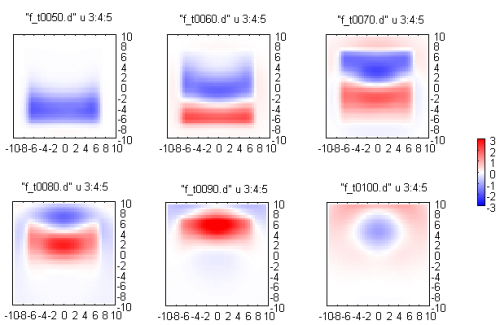
Для того, чтобы получить подобные картинки в частотном представлении, нужно использовать сразу два битовых флага DET_F и DET_TSTEP:
task.AddDetectorSet("ff",Vector_3(-9.5),Vector_3(9.5),iVector_3(1,20,20),DET_F|DET_TSTEP);
Как видно, в С++ битовые флаги можно объединять с помощью оператора |.
Добавление тела
Добавим стеклянную (показатель преломления , а диэлектрическая проницаемость
) сферу радиуса 5 в центр контейнера:
task.AddObject(emMedium(1.45*1.45),new Sphere(5,Vector_3()));
Желательно, чтобы между телом и границей TF/SF было расстояние не меньше 1.5 сеточных шагов по пространству. Мы это условие соблюдаем (7-5=2).
После этого можно вновь создать фильм и увидеть, как сфера частично рассеивает падающую волну в область Scattered Field. Рассеянная волна через какое-то время поглощается PML, что свидетельствует о том, что эксперимент можно заканчивать. Что мы и делаем, выбрав время эксперимента 200.
Если бы вместо PML мы бы использовали отражающие граничные условия, то рассеянная волна переотражалась бы от границ контейнера.
task.SetBC(BC_REFL,BC_REFL,BC_REFL);
Это также можно увидеть с помощью фильма, который также можно построить в качестве домашнего задания.
gnuplot позволяет рисовать линии, вставлять надписи, регулировать размеры осей, а также их наличие. Это позволяет делать достаточно красивые фильмы. Вот один из них.
В этом фильме свет падает под углом к осям y,z. Для того, чтобы отчетливей была видна рассеянная сферой волна, мы увеличили расстояние между сферой, границей TF/SF и PML.
Поток энергии через поверхность
Прежде чем читать дальше, ознакомьтесь с теорией.
Программа FDTD позволяет рассчитать поток энергии заданную поверхность. Для этого на этой поверхности размещается сетка детекторов, данные которых участвуют в расчете этого потока. Такой поверхностью может являться поверхность параллелепипеда
task.AddFluxSet("flux",Vector_3(-8.5),Vector_3(8.5));
Созданные детекторы будут находиться друг от друга примерно на расстоянии одного сеточного шага.
Мы создали поверхность в области Scattered-Field для того, чтобы рассчитать поток энергии отраженной от сферы волны . Желательно, чтобы между детекторами и границей TF/SF было расстояние не меньше 1.5 сеточных шагов по пространству. Мы это условие соблюдаем (8.5-7=1.5).
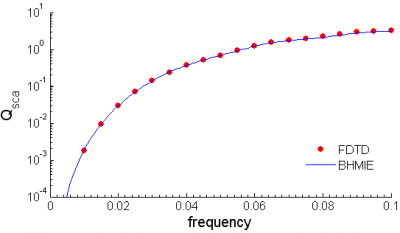
После анализа будет создан файл flux.d с двумя колонками для частоты и соответствующего потока энергии. Его можно использовать для расчета эффективности рассеяния для нашей стеклянной сферы, который равен
,
где
- поток энергии рассеянной волны через окружающую сферу поверхность
- интенсивность падающей волны
- площадь проекции сферы на плоскость перпендикулярную направлению падающей волны.
Для расчета интенсивности падающего света мы можем воспользоваться полученным ранее файлом cf_r0000.d, в котором хранится падающее поле в частотном представлении. Поскольку падающая плоская волна поляризована в направлении x, ее интенсивность можно получить как .
Ниже придставлено сравнение для между FDTD и программой BHMIE. Значения
представлены в логарифмическом масштабе.
Программа BHMIE основана на суммировании рядов, составляющих аналитическое решение задачи рассеяния на сфере (решение этой задачи было опубликовано Ми в 1908 г.). Описание программы BHMIE можно найти в книге 1). Сама программа (вместе с другими замечательными программами) скачивается отсюда: http://atol.ucsd.edu/scatlib/index.htm, где она любезно выложена Dr Piotr J. Flatau из University of California San Diego.
Просмотр заданной геометрии
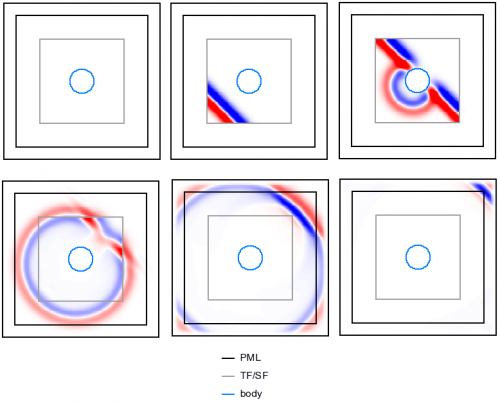
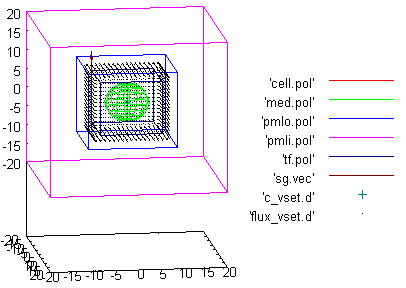
Для того чтобы можно просматривать в gnuplot расположение задаваемых объектов, программа на выходе создает некоторые вспомогательные файлы. Перечислим их:
- cell.pol – вычислительный объем
- med.pol – тела
- pmli.pol, pmlo.pol - внутрення и наружняя границы PML
- tf.pol – область Total Field
- sg.vec – направление падающей волны
- файлы с суффиком _vset - детекторы
Расширение pol в имени файлов означает, что в файлах задается многогранник(и) (polyhedron), расширение d - точки (dot), а расширение vec - вектора (vector).
Наберем в командной строке gnuplotа
gnuplot> sp 'cell.pol' w l, 'med.pol' w l, 'pmlo.pol' w l, 'pmli.pol' w l, 'tf.pol' w l, 'sg.vec' w vec, 'c_vset.d', 'flux_vset.d' w d
В результате мы увидим следующее.
Преобразование ближнего поля в дальнее
Прежде чем читать дальше, ознакомьтесь с теорией.
Для расчета углового распределения рассеянной волны используется матрица амплитуд рассеяния, связывающая амплитуду рассеянного поля в дальней зоне с амплитудой падающей волны. Для получения рассеянного поля в дальней зоне можно было бы значительно увеличить вычислительный объем, так чтобы он захватывал собой дальнюю зону. Однако имеется более экономный путь.
Окружим тело мыслимой замкнутой поверхностью в области Scattered-Field. Значение поля вне этой поверхности в начальный момент времени равно нулю. В течение численного эксперимента нам становится известно значение поля на поверхности при
. Из свойств уравнений Максвелла вытекает, что этого достаточно для однозначного определения поля вне поверхности при
. Это можно сделать с помощью техники преобразования ближнего поля в дальнее (Near-to-Far-Field Transformation). В EMTL эта техника реализована так, что на выходе вы получите дальние поля сразу в частотном представлении.
Окружим тело замкнутой поверхностью в области Scattered-Field (она совпадает с поверхностью, использованной нами ранее для расчета потока рассеянной волны).
Vector_3 origin; // центр, откуда отмеряется расстояние до "дальних" точек valtype length=1000; // расстояние до "дальних" точек // сетка по углам valtype th0=0,th1=M_PI; valtype fi0=0,fi1=M_PI/2; int thn=19,fin=2; task.AddNearToFarSet("far",Vector_3(-8.5),Vector_3(8.5),origin,length,th0,th1,thn,fi0,fi1,fin,DET_TSTEP);
Значения полей на этой поверхности, полученные в ходе численного эксперимента, будут использоваться на этапе анализа для получения полей в точках, удаленных на расстояние 1000 от начала координат в направлениях, задаваемых углами и
. Угол
пробегает значения от 0 до
с шагом
, а угол
принимает значения 0 и
.
По окончанию анализа создадутся файлы 'far_xxxx.d, где xxxx – номер частоты (частоты нумерются по возрастанию). Поля и
в этих файлах будут разложены по ортонормированному базису, связанному со сферической системой координат (см. описание).
Сделаем несколько замечаний по поводу содержимого 'far.d'.
Во-первых, близко к нулю, что согласуется с тем фактом, что рассеянное поле в дальней зоне поперечно.
Во-вторых, близко к нулю для угла
, а
близко к нулю для угла
. Это связано с тем, что недиагональные элементы матрицы амплитуд рассеяния для сферы равны нулю:
.
Отметим также, что при рассеянии на сфере матричные элементы не зависят от угла
.
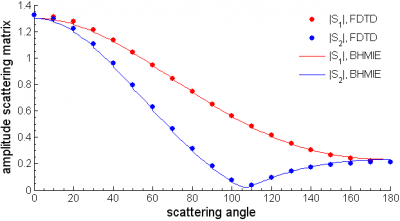
Теперь, пользуясь абсолютным значением из файла cf_r0000.d, а также принимая во внимание изложенную здесь теорию, мы можем вычислить абсолютные значения элементов
.
Ниже представлено сравнение полученных результатов с результатами программы BHMIE для частоты . Заметим, что для углов
близких к
согласие хуже. Это явление известно в литературе по FDTD под названием Backscattering Problem.
Фазы работы
Как можно видеть из вышесказанного, объект uiExperiment может последовательно находиться в следующих трех фазах:
- Построение геометрии. На этой фазе вы должны определить размер вычислительного объема, шаг по сетке и граничные условия, а также задать тела, источники и детекторы.
- Расчет, протекающий во время работы функции Calculate
- Анализ, вызываемый функцией Analyze. На этой фазе производится анализ выходных двоичных файлов, созданных в ходе расчета. На основании этих двоичных файлов создаются читаемые текстовые файлы.
Иногда бывает полезно, чтобы были пройдены не все фазы. Для этого нужно использовать функцию SetPhases, параметр которой может принимать значения «g», «c» и «a». Например, если вы укажете
task.SetPhases("g");
то будет пройдена только фаза построения геометрии. Это полезно, если вы хотите ознакомиться с построенной геометрией в gnuplot без проведения самого расчета (например, чтобы проверить, правильно ли она задана).
Значение «c» и приведут к тому, что будет выполнено построение геометрии и расчет. Это полезно, если вы хотите отложить анализ больших двоичных файлов на потом (например, когда задача будет перезапущена на другом числе процессоров).
Значение «a» означает выполнение только фазы анализа.
Спектры прохождения и отражения для периодических структур
С помощью FDTD можно рассчитывать спектры прохождения и отражения для периодических структур (фотонные кристаллы, массивы антенн и т.д.) Для их расчета рассчитывается распространение ограниченного по времени импульса через структуру. Периодичность моделируется путем задания периодических граничных условий в нужных направлениях.
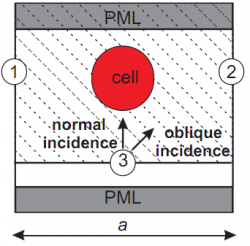
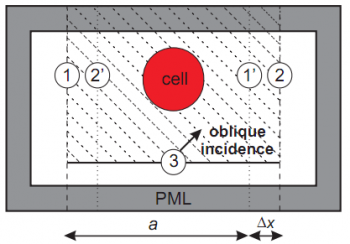
Рассмотрим элементарную ячейку фотонно-кристаллической пластинки, состоящей из сфер упакованных в квадратную решетку. Такая ячейка ограничена периодическими границами 1 и 2. Граница Total Field / Scattered Field (TF/SF) 3 генерирует падаюший импульс (область Total Field заштрихована). Для непериодического направления используются поглощающие граничные уловия PML. Они поглощают отраженную и прошедшую волны, моделируя их уход на бесконечность. Численный эксперимент ведется до тех пор пока излучение не выйдет из структуры. Прошедшая и отраженная волны записываются во время эксперимента, преобразуются в частотное представление и нормализуются на спетр падающей волны, что дает спектры прохождения и отражения.
В случае нормального падения периодические граничные условия выглядят так
где это электрическое или магнитное поле (
или
),
это вектор трансляции для периодической структуры,
и
пространственная и временная координаты.
В случае наклонного падения периодические граничные условия содержат временной сдвиг. В 2D они принимают форму
где это угол падения,
- скорость света в среде, откуда падает свет.
Смысл этого выражения легко понять из следующих соображений.
Падающий импульс приходит на границу 1 раньше чем на границу 2, поэтому значения полей на этих границах «сдвинуты во времени» относительно друг друга.
Использование периодических граничных условий требует знания поля в прошлом на границе 1 (для применения на границе 2) и поля в будущем на границе 2 (для применения на границе 1).
Поле в прошлом могут быть получено, если ведется запись распространения волны.
Получение поля в будущем проблематично, поскольку оно неизвестно заранее.
Для решения этой проблемы можно использовать итерационный метод для моделирования наклонного падения на периодическую структуру.
Ниже мы рассматрим моделирование нормального падения на одномерном примере, далее мы объясним принцир итерационного метода и покажем как он наботает на примере фотонно-кристаллической пластинки из сфер и антиотражающего текстурированного покрытия.
Бесконечная пластинка
Ниже мы рассмотрим как рассчитать спектры прохождения и отражения для бесконечной пластинки (которая может рассматриваться как периодическая с периодом нуль) в случае нормального падения.
Создадим объект этого класса uiExperiment:
uiExperiment task;
Будем считать, что пластинка бесконечна вдоль направлений x и y, и конечна вдоль направления z.
Размер вычислительного объема вдоль напрвления z будет равным 3. Шаг по сетке равен 0.05. Мы используем поглощающие граничные условия вдоль z.
task.SetInternalSpace(Vector_3(0,0,0),Vector_3(0,0,3)); task.SetResolution(0.05,1); task.SetBC(BC_PER,BC_PER,BC_PML);
Мы указали нулевой размер вычислительного объема вдоль направлений x и y, поскольку наша задача фактически одномерна. На самом деле в нашем случае толщина вдоль этих направлений будет равна двум шагам сетки по оставшемуся направлению z. Граничные условия вдоль x и y будут периодическими, тем самым моделируя одномерность.
Фактор Куранта должен быть не больше , где
это размерность задачи.
Мы используем фактор Куранта 1 (второй аргумент SetResolution), что допустимо в силу одномерности задачи.
Мы могли бы взять меньшее значение, но тогда шаг по времени был бы меньше.
Световой импульс падает на пластинку снизу вдоль направления z. Для генерации импульса зададим область Total Field в виде полупространства, ограниченное снизу плоскостью, которая перпендикулярна оси z и пересекает ее в точке 0.5.
task.AddTFSFPlane(INF,INF,0.5);
Плоская волна распространяется вдоль оси z, вектор поляризации направлен вдоль оси x.
task.SetPlaneWave(Vector_3(0,0,1),Vector_3(1,0,0));
В прошлом примере со сферой мы задавали явно временную зависимость падающего импульса в форме Беренгера с заданными параметрами. В этот раз мы не будем ее задавать. По умолчанию будет использоваться форма Беренгера с такими параметрами, чтобы спектр импульса хорошо покрывал длины волн, на которые приходится более 10 сеточных шагов.
Поставим по одному детектору в область Scattered Field перед пластинкой и в область Total Field за пластинкой.
task.AddDetectorSet("h",Vector_3(0,0,0.25),Vector_3(0,0,2.75),iVector_3(1,1,2));
Для расчета спектра потока вектора Пойнтинга отраженной и прошедшей волны мы поставим плоскости детекторов, перпендикулярные направлению z и пересекающие ось z в точках 0.25 и 2.75.
task.AddRTASet("flux",2,0.25,2.75);
Направления в функции AddRTASet задаются следующим образом: x – 0, y - 1, z – 2. Поэтому второй аргумент означает z.
Поскольку поток вектора Пойнтинга падающей волны расчитывается программой автоматически по форме падающего импульса, для его расчета детекторов не требуется.
Проведем расчет.
task.Calculate(100); task.Analyze();
В результате граница TF/SF сгенерирует плоский импульс, который будет беспрепятственно распространяться вдоль направления z и в конце концов поглотится в PML. Детектор в зоне Total Field фиксирует распространяющийся импульс Беренгера
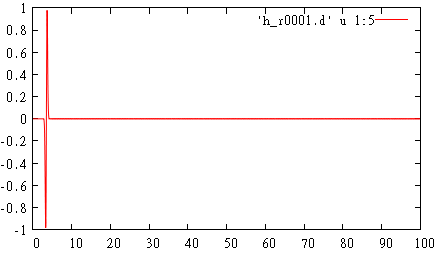
gnuplot> p 'h_r0001.d' u 1:5 w l
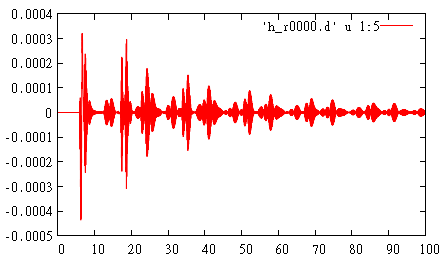
Детектор в области Scattered Field фиксирует сигнал, отразившися от PML, который имеет амплитуду порядка 1е-4 от исходного сигнала (PML работает неидеально и что-то отражает). Однако это амлитуда мала и практически не влияет на результаты.
gnuplot> p 'h_r0000.d' u 1:5 w l
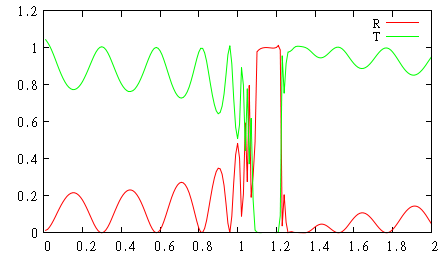
В файле flux.d будут представлены потоки вектора Пойнтинга отраженной, падающей и прошедшей волны соответственно. Их можно использовать для простроения спектра отражения и прохождения
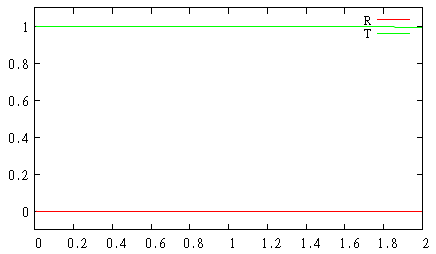
gnuplot> p [][-.1:1.1] 'flux.d' u 1:($2/$3) w l t 'R', 'flux.d' u 1:($4/$3) w l t 'T'
Как мы видим, отражение равно нулю, а прохождение – единице.
Зададим плоскопараллельную пластинку
emMedium M(2.25); M.AddPolarizability(emLorentz(1.1*(2*M_PI), 1e-5*(2*M_PI), .5)); M.AddPolarizability(emLorentz(.5*(2*M_PI), .1*(2*M_PI), 2*1e-5));
task.AddObject(M,GetPlate(Vector_3(0,0,1),Vector_3(0,0,1),1));
Пластинка задается функцией GetPlate, первый аргумент которой задает направление вдоль пластинки (направление z), второй точку, через которую проходит одна из сторон пластинки, а третий - толщину пластинки (она равна 1). Пластинка сделана из дисперсной среды, описываемой двумя членами Лоренца.
Повторив расчет, мы получим спектр отражения и прохождения для пластинки.
gnuplot> p 'flux.d' u 1:($2/$3) w l t 'R', 'flux.d' u 1:($4/$3) w l t 'T'
Мы видим, что результаты для маленьких частот неточны (прохождение больше 1). Эту ситуацию можно исправить, выбрав более широкий по времени импульс Беренгера, который покроет маленькие частоты.
task.SetSignal(new Berenger(1,2.5,.5,12.5));
Однако, в этом случае ухудшатся результаты для более высоких частот, в чем вы можете сами убедиться.
Поглощение может быть получено как 1 - R - T.
Расстояние между телами, границей TF/SF, PML и детекторами должно быть не менее 2 сеточных шагов. В нашем примере мы придерживались большего расстояния (5-20 сеточных шагов), поскольку иногда это может улучшить результат.
Кремниевая подложка
Ниже мы рассчитываем отражение от полубесконечной кремниевой подложки в случае нормального падения. Мы используем уже имеющийся код из предыдущей подсекции (задание граничных условий, области Total Field и т. д.)
Для задания полубесконечной подложки мы можем воспользоваться функцией GetHalfSpace. В отличие от пластинки, у подложки нет второй замыкающей поверхности, и она бесконечно продолжается вдоль оси z. В модели FDTD она погружается в PML, что моделирует ее бесконечность.
Материалом подложки будет кремний. Для получения соответствующего объекта emMedium можно воспользоваться функцией getSi, у которой имеется аргумент, по умолчанию равный единице. Этот аргумент задает, чему равна единица длины FDTD в микронах. Это необходимо для правильной калибровки коэффициентов, участвующих в расчете диэлектрической проницаемости (см. как задавать среды в EMTL). В нашем случае единица FDTD будет равна 0.1 микрона.
task.AddObject(getSi(.1),GetHalfSpace(Vector_3(0,0,1), Vector_3(0,0,1)));
Параметры, используемые для апроксимации диэлектрической проницаемости кремния функцией getSi, были получены с помощью программы на MatLab, которую вы можете найти в разделе Фитинг диэлектрической проницаемости.
По умолчанию в качестве PML используется тип UPML (Uniaxial PML). Однако, в него можно погружать только диэлектрические среды. Поскольку мы погружаем в PML дисперсную среду (кремний), мы должны использовать CPML (Convolutional PML). Он работает несколько медленнее, чем UPML, но является более универсальным.
task.SetPMLType(CPML_TYPE);
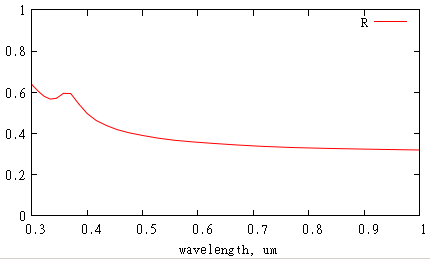
Построим зависимость отражения от кремниевой подложки от длины волны в мкм.
gnuplot> set xlabel 'wavelength, um' gnuplot> p [.3:1][0:1] 'flux.d' u (.1/$1):($2/$3) w l t 'R'
Как видно, кремний достаточно сильно отражает в оптическом диапазоне. Для уменьшения отражения могут использоваться антиотражающие текстурированные покрытия.
Наклонное падение
Итерационный метод для моделирования наклонного падения на периодическую структуру подразумевает проведение нескольких численных экспериментов FDTD, которые мы называем итерациями. В течение каждой итерации происходит запись значений полей на периодических границах. Это дает ключ к решению проблемы получения полей из будущего: поля в будущем известны из прошлой итерации, поскольку они были уже записаны. При этом поля из прошлого могут браться из текущей итерации. Для управления итерационным процессорм используется метод Total Field/Scattered Field (TF/SF). Спустя некоторое число итераций граница TF/SF работает как применение периодических граничных условий с нужным сдвигом во времени.
Наш метод описан в статье httpPDF
Проиллюстрируем работу итерационного метода на примере расчета наклонного падения на фотонно-кристаллическую пластнику из упакованных в квадратную решетку сфер.
Мы используем метод Total Field/Scattered Field (TF/SF) для генерации плоской волны внутри области Total Field, которая заштрихована на рисунке.
TF/SF граничные условия на границе 3 задают наклонно падающую волну, которая известна заранее.
Идея итерационного метода заключается в применении дополнительной TF/SF генерации на границах и
, используя записанные значения полей из точек-образов
и
.
Для отрицательного временного сдвига (поля из прошлого) можно брать поля из текущей итерации
, тогда как для положительного временного сдвига (поля из будещего) мы используем поля, записанные на предыдушей итерации:
Расстояние между границами 1 и 2 больше периода на некоторую величину
равную нескольким сеточным шагам. Это нужно для разделения границ TF/SF 1, 2 и точек-образов.
На первой итерации «падающая волна» на границах TF/SF 1, 2 есть нуль.
Более подробно про итерационный метод можно прочитать здесь httpPDF
Для включения итерационного метода нужно использовать функцию SetOblique. Первый параметр этой функции есть число итераций. Второй параметр (назовем его n) отвечает за работу детекторов: детекторы работают и анализируется на каждой n-ой и на последней итерации. Текстовые файлы детекторов с промежуточных итераций помечаются суффиксом «_i» (i это номер итерации) после имени детектора.
Ниже мы приводим код для моделирования наклонного падения в вакууме, рассматривается двумерный случай (размер вычислительного объема в направлении x есть нуль).
#include "uiexp.h" int main(int argc,char **argv){ emInit(argc,argv); uiExperiment task; task.SetInternalSpace(Vector_3(.5,0,0),Vector_3(.5,2,3)); task.SetResolution(.05); task.SetBC(BC_PER,BC_PER,BC_PML); theta=45*M_PI/180.; // angle of incidence, radians. theta=0 corresponds to normal incidence Vector_3 k=Vector_3(0,sin(theta),cos(theta)); // light propagation direction Vector_3 E(1,0,0); // s polarization // Vector_3 E(0,cos(theta),-sin(theta)); // p polarization task.AddTFSFPlane(INF,INF,.5); task.SetPlaneWave(k,E); task.SetOblique(10,1); // comment it for normal incidence task.BuildDimensions(); Vector_3 p1,p2; task.GetSpace(p1,p2); Vector_3 mv1=p1+.05, mv2=p2-.05; // one mesh step from the calculated volume border mv1[0]=mv2[0]=(p1[0]+p2[0])/2; task.AddDetectorSet("movie",mv1,mv2,INT_INFTY,DET_TSTEP); task.CalculateN(300); task.Analyze(); return 0; }
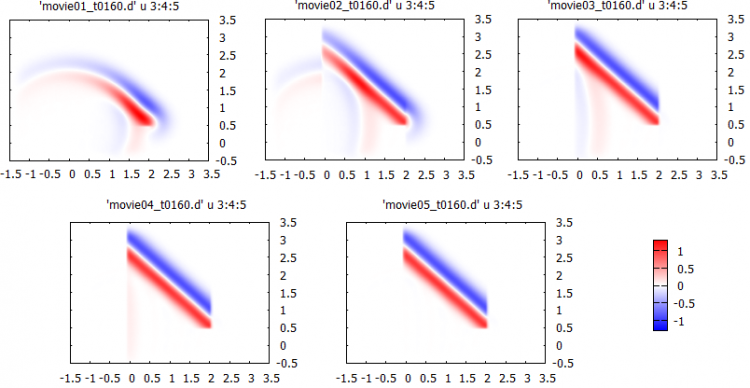
Заметим, что фактический размер вычислительного объема больше чем тот, который задан в аргументах функции SetInternalSpace. Этот размер включает в себя PML и пространство слева от границы 1 и справа от границы 2. Фактический размер вычислительного объема можно получить с помощью функции GetSize. Для иллюстрации сходимости метода, мы поставили детекторы «movie» по всему вычислительному объему. В течение численного эксперимента мы получим множество файлов moviexx_tyyyy.d, где xx это номер итерации, а yyyy это временной шаг. Эти файлы можно использовать для построения эволюции распространения поля на разных итерациях.
gnuplot> set pm3d interpolate 2,2 gnuplot> cbr=1.3 gnuplot> set palette defined (-cbr 'blue', 0 'white', cbr 'red') gnuplot> set cbrange [-cbr:cbr] gnuplot> set view 0,0 gnuplot> sp 'movie01_t0160.d' u 3:4:5 w pm3d
Как можно видеть из рисунка, в нашем случае распределение поля на 160 временном шаге сходится к решению (плоский импульс в вакууме) за первые 5 итераций. Для получения решения на более позднем временном шаге требуется больше итераций.
Фотонно-кристаллическая пластинка
Фотонно-кристаллическая пластинка это структура конечная вдоль одного направления и периодическая вдоль остальных направлений.
Ниже мы моделируем наклонное падение на такую пластинку состояющую из металлических (,
) сфер упакованных в квадратную решетку.
Период решетки
, радиус сфер
, сеточный шаг равен 0.025.
#include "uiexp.h" int main(int argc,char **argv){ emInit(argc,argv); uiExperiment task; task.SetInternalSpace(0,Vector_3(1,1,3)); task.SetResolution(.025); task.SetBC(BC_PER,BC_PER,BC_PML); valtype theta=45*M_PI/180.; // angle of incidence, radians. theta=0 corresponds to normal incidence Vector_3 k(0,sin(theta),cos(theta)); Vector_3 E(1,0,0); // s polarization // Vector_3 E(0,cos(theta),-sin(theta)); // p polarization task.AddTFSFPlane(INF,INF,.5); task.SetPlaneWave(k,E); task.SetOblique(100,1); task.AddObject(emMedium(4,2),new Sphere(.375,Vector_3(.5,.5,1.5))); task.AddDetectorSet("h",Vector_3(.5,.5,0.25),Vector_3(.5,.5,2.75),iVector_3(1,1,2)); task.AddRTASet("flux",2,0.25,2.75); task.CalculateN(2000); task.Analyze(); return 0; }
Посмтроим геометрию в gnuplotе:
gnuplot> sp 'cell.pol' w l, 'med.pol' w l, 'pmlo.pol' w l, 'pmli.pol' w l, \ gnuplot> 'tf.pol' w l, 'sg.vec' w vec, 'itf.pol' w l, 'unit.pol' w l
Согласно картинке выше, 'itf.pol' соответствует границам 1 и 2, а 'unit.pol' соответствует периодической ячейке ширины a (она ограничена границей между 1 and 2' и границей между 1' и 2).
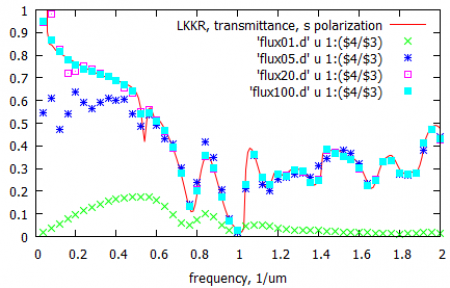
Сравним результаты для спектра прохождения, полученные с помощью FDTD и полуаналитического метода layer Korringa-Kohn-Rostoker (LKKR).
Как можно видеть из сравнения, результаты для больших частот сходятся быстрее. При этом 5-10 итераций достаточно для получения спектра прохождения с нормальной точностью. Для окончательной сходимости метода в нашем случае требуется порядка 100 итераций. Вообще, число итераций, необходимое для сходимости метода, пропорционально числу временных шагов в численном эксперименте (в нашем примере это 2000).