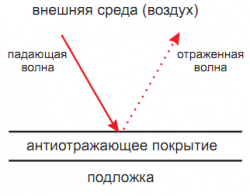
Антиотражающие текстурированные покрытия
Во многих практических приложениях возникает необходимость уменьшения коэффициента отражения от границы между двумя средами. В солнечной энергетике уменьшение отражения от фотоэлемента позволяет существенно увеличить его КПД. В биноклях, телескопах и фотографических приборах уменьшение отражения приводит к увеличению светопропускания и контраста оптического изображения. Уменьшение отражения важно в целях устранения блика от дисплеев, а также при использовании контактных линз для увеличения видимости глаз. В авиационной технике уменьшение отражения требуется в целях маскировки боевых самолетов и вертолетов, чтобы позволять им проникать незамеченными в воздушное пространство противника.
Одним из способов уменьшения отражения является просветление оптики, заключающееся в создании на поверхности тела оптически тонкой пленки. Принцип ее действия основан на взаимном гашении интерферирующих друг с другом лучей, которые отражаются от наружной и внутренней сторон пленки. У однослойных просветляющих покрытий имеется серьезный недостаток: они могут быть использованы только для узкого диапазона длин волн и углов падения. Этот диапазон можно расширить, применяя многослойные покрытия. Принцип действия таких покрытий тот же, что и у однослойных, - взаимное интерференционное гашение двух или нескольких волн, отраженных от разных границ раздела между слоями. Конкретные значения толщин слоев и их показателей преломления могут подбираться в зависимости от желаемого эффекта: близкий к нулю коэффициент отражения в широкой спектральной области или в широком диапазоне углов для заданной длины волны. Недостатком многослойных покрытий является проблематичность нахождения материалов с нужной диэлектрической проницаемостью.
Альтернативой к многослойным просветляющим покрытиям могут служить слои с непрерывно меняющимся коэффициентом преломления. Применение таких покрытий позволяет достичь низких значений коэффициента отражения в широком спектральном диапазоне. Однако и у этого метода есть свои недостатки, среди которых несоответствие температурных коэффициентов расширения получаемых слоев и адгезия.
Добиться плавного изменения показателя преломления можно с помощью текстурирования поверхности, то есть создания на ней массива из конусообразных рассеивателей или двумерных канавок. Такой способ был впервые обнаружен при изучении структуры глаза некоторых видов мотыльков. Наружная поверхность роговицы глаза таких мотыльков, играющая роль линзы, покрыта сетью конусообразных пупырышек, называемых роговичными сосками, обычно высотой нм и примерно таким же расстоянием между ними
. Поскольку длина волны видимого света
больше размера пупырышек, их оптические свойства могут описываться с помощью приближения эффективной среды. Согласно этому приближению свет распространяется через них так же, как если бы он распространялся через среду с непрерывно меняющейся эффективной диэлектрической проницаемостью. Это в свою очередь приводит к уменьшению коэффициента отражения, что позволяет мотылькам хорошо видеть темноте, а также оставаться незамеченными для хищников вследствие уменьшения отражательной способности от глаз.

Роговица глаза ночного мотылька.
Текстурированная поверхность обладает антиотражающими свойствами также и в коротковолновом пределе, при длинах волн много меньших характерного размера текстуры. Это связано с тем, что лучи, первоначально отразившиеся от текстурированной поверхности, имеют шанс все же проникнуть в среду при последующих переотражениях. При этом текстурирование поверхности создает условия, при которых прошедший луч может отклониться от нормали, что ведет к эффекту запутывания прошедшего света (англ. - light trapping), используемому, например, в солнечных элементах.
Теоретическое и экспериментальное исследование свойств текстурированных поверхностей активно ведется уже начиная с 70х гг. прошлого века. Однако, интерес к этой области особенно возрос в последнее время, а именно, появилась масса новых работ по успешному изготовлению антиотражающих нанотекстурированных покрытий, используемых, в частности, в производстве солнечных элементов.
Дальнейшее изложение будет построено следующим образом. Вначале мы изложим теоретические результаты касательно оптических свойств текстурированных поверхностей в длинно- и коротковолновом пределах. Затем мы исследуем антиотражающие свойства текстурированной поверхности во всем диапазоне размеров текстуры с помощью FDTD.
Хорошее изложение данного материала можно также найти здесь: http PDF
Приближение эффективной среды
В случае, когда характерная длина волны много больше размера составляющих текстуру рассеивателей, оптические свойства текстурированной поверхности могут описываться в приближении эффективной среды. Как уже говорилось ранее, в рамках этого приближения свет распространяется через текстурированную поверхность так, как если бы он распространялся через пленку с непрерывно меняющейся эффективной диэлектрической проницаемостью.
Поскольку приближение эффективной среды будет применяться в некоторых наших дальнейших вычислениях, мы опишем ниже имеющиеся способы расчета эффективной диэлектрической проницаемости. По этой же причине мы изложим используемые нами в дальнейшем способы расчета коэффициента отражения от пленки с непрерывно меняющейся диэлектрической проницаемостью. Далее в этом параграфе мы приведем основные имеющиеся в литературе результаты, полученные с использованием приближения эффективной среды.
Изложение способа расчета эффективной диэлектрической проницаемости для текстурированной поверхности будет состоять из нескольких шагов. Вначале мы опишем, как может быть посчитана эффективная диэлектрическая проницаемость для структуры бесконечной в направлении , так что ее диэлектрическая проницаемость
зависит только от
,
. Потом мы рассмотрим случай плоскопараллельного слоя, имеющего конечный размер по
. Далее мы покажем, как может быть посчитана эффективная диэлектрическая проницаемость для многослойных плоскопараллельных структур, и наконец перейдем к структурам с непрерывным профилем, которыми и являются текстурированные поверхности.
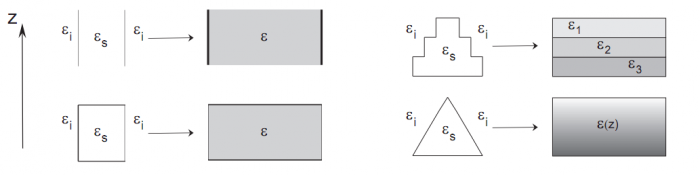
Рассмотрим первый случай, когда диэлектрическая проницаемость структуры периодична по направлениям
и
и не зависит от
. При соответствующем выборе осей
и
эффективная диэлектрическая проницаемость представляется в виде тензора
, у которого имеются только три ненулевые отличные друг от друга диагональные компоненты
,
и
. В случае наличия центральной симметрии в плоскости
две первые компоненты равны
.
В некоторых случаях для эффективной диэлектрической проницаемости существуют простые приближенные выражения.
Рассмотрим вначале случай последовательности параллельных пластин, когда зависит только от одной координаты. Пусть
- толщина каждой пластины,
- расстояние между ними,
- диэлектрическая проницаемость каждой из пластин, а
- диэлектрическая проницаемость окружающей их среды.
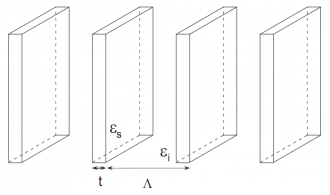
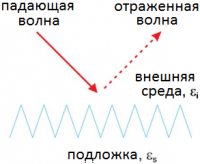
Регулярная последовательность тонких параллельных пластин.
В предположении, что расстояние между пластинами мало по сравнению с длиной волны
, поле в пластинах и между ними можно считать однородным. Тогда из требований непрерывности на границах пластин нормальной составляющей вектора
и тангенциальной составляющей вектора
для компонент тензора
, соответствующих перпендикулярным и параллельным к пластинам направлениям, можно получить
где и
- доли общего объема, занимаемые пластинами и окружающей средой соответственно.
Так как эффективная диэлектрическая проницаемость одинакова для всех направлений, параллельных пластинам, но различна для направлений, перпендикулярных к ним, наша система ведет себя как одноосный кристалл с оптической осью, нормальной к плоскостью пластин.
Рассмотрим теперь структуру, представляющую бесконечно вытянутые в направлении параллелепипеды с квадратными основаниями, упакованные в квадратную решетку.
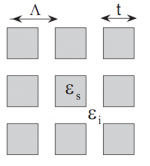
Бесконечно вытянутые параллелепипеды с квадратными основаниями, упакованные в квадратную решетку.
Для такой структуры эмпирически было подобрано следующее выражение для эффективного коэффициента преломления в направлениях и
:
где - есть простое усреднение коэффициента преломления, а
и
получаются взятием корня из величин
где , а
и
рассчитываются согласно предыдущим выражениям для пластин.
Для бесконечно вытянутых параллельных друг другу цилиндров эффективная диэлектрическая проницаемость может быть рассчитана по формуле Максвелла-Гарнетта:
где - фактор заполнения цилиндров по пространству.
Отметим, что в двух последних рассмотренных нами случаях, эффективная диэлектрическая проницаемость для волн, поляризованных в и
направлениях, одинакова по причине наличия центральной симметрии в плоскости
. Таким образом, эффективная диэлектрическая проницаемость задается тензором
, у которого имеются только две ненулевые отличные друг от друга диагональные компоненты
и
. При этом компонента
получается с помощью простого усреднения, что можно показать из тех же соображений непрерывности тангенциальной составляющей электрического поля, которые применяются при выводе выражения
для пластин.
До сих пор мы предполагали, что структура бесконечна вдоль направления . Однако, когда толщина структуры вдоль направления
много больше критического значения
, влиянием конечности структуры можно пренебречь.
Приближением эффективной среды также можно пользоваться при описании многослойных структур. Для этого каждый слой рассматривается отдельно и для него находится своя эффективная диэлектрическая проницаемость.
Приближение эффективной работает также для структур с непрерывным профилем. Точного теоретического обоснования для этого в литературе нет, однако этот подход с успехом применяется во многих работах при описании текстурированных поверхностей.
Итак, в приближении эффективной среды оптические свойства текстурированной поверхности подобны свойствам неоднородной слоистой среды. В дальнейших расчетах коэффициента отражения от такой среды могут использоваться два метода.
Первый метод заключается в разбиении неоднородной среды на совокупность слоев малой толщины, в каждом из которых значение диэлектрической проницаемости можно приблизительно считать постоянным. Для каждого слоя находится матрица перехода, а далее путем перемножения этих матриц получается матрица перехода для всей совокупности слоев. С помощью этой матрицы может быть получен коэффициент отражения. Подробное обоснование и описание работы этого метода можно найти в 1).
Для нахождения коэффициента отражения может применен другой метод, основанный на непосредственном решении уравнений Максвелла в неоднородной среде2).
Приближение геометрической оптики
Оптические свойства текстурованных поверхностей в коротковолновом пределе могут быть описаны приближением геометрической оптики. Для численного моделирования в этом приближении широко используется метод трассировки лучей. Этот метод заключается в запуске множества геометрических лучей и отслеживании взаимодействий каждого из них с заданными поверхностями.
Оптимизация геометрии
В дальнейшем мы рассматриваем подложку с нанесенными на нее стеклянными пирамидками (коэффициент преломления ) с высотой
.
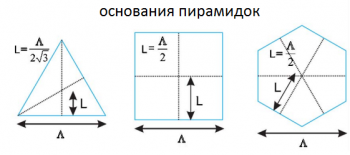
Основаниями пирамидок являются треугольники, шестиугольники, квадраты и круги (в этом случае пирамидка вырождается в конус). Расстояние между боковой стороной основния пирамидки и ее центром есть . Пирамидки плотно упакованы в квадратную или треугольную решетки с периодом
.
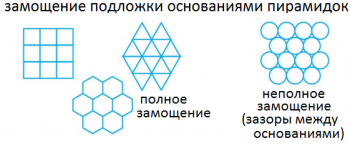
Мы будем отдельно выделять два случая: случай полного замощения подложки основаниями пирамидок (это соответствует плотной квадратной или треугольной упаковки пирамидок с квадратными или треугольными основаниями соответственно) и случай неполного замощения (это соответствует конусам, поскольку между их круглыми основаниями всегда имеется зазор). Мы рассматриваем случай нормального падения.
Приближение эффективной среды
Как уже говорилось ранее, в длинноволновом пределе , оптические свойства текстурированной поверхности подобны свойствам промежуточного слоя с непрерывно меняющейся диэлектрической проницаемостью. Увеличение отношения высоты пирамидок к длине волны
приводит к увеличению плавности изменения эффективной диэлектрической проницаемости и соответственно к уменьшению отражения.
Рассмотрим вначале случай полного замощения, для которого фактор заполнения у вершин пирамидок , а у оснований
. Вследствие этого согласно имеющимся выражениям для эффективной диэлектрической проницаемости
и
, где
есть диэлектрическая проницаемость внешней среды, а
есть диэлектрическая проницаемость текстурированного покрытия.
Отметим, что подбирая специальную форму профиля пирамидок можно изменять степень убывания отражения при увеличении
.
Например, если задавать многочленом степени
таким, что его производные
, то отражение
.
В частности для профилей
и
(мы предполагаем
) мы получаем
и
.
Подберем такой специальный профиль, который бы характеризовался равенством нулю всех производных в точках
и
. Без ограничения общности положим
. Возьмем за основу бесконечно дифференцируемую функцию
, которая вместе со всеми своими производными равна нулю в
. Функция
будем обладать теми же свойствами в
. Далее, несложно заметить, что одновременно этими свойствами в
и
обладает функция
. Однако эта функция равна нулю в
и
, а нам бы хотелось, чтобы в
она была бы равна единице и задавала таким образом профиль пирамидки. Для этого можно ее проинтегрировать и получить в итоге профиль
, где значение константы
побирается таким, чтобы
. В случае такого «интегрального» профиля коэффициент отражения при увеличении
уменьшается экспоненциально, поскольку
.
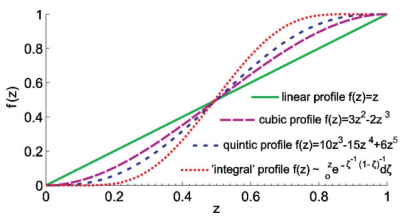
Мы провели численные расчеты для плотно упакованных квадратных пирамидок с профилями:
- ,
. Мы использовали плоские пирамиды, в которых ширина линейно зависит от высоты. Поскольку фактор заполнения пропорционален ширине в квадрате, мы использовали
;
- ,
;
- ,
.
В соответствии с приведенными рассуждениями, для этих случаев было получено ,
и
соответственно. Отметим, что результаты, полученные с помощью приближения эффективной среды и FDTD находятся в хорошем согласии друг с другом.
Мы рассчитали отражение от дифракционной решетки с интегральнам профилем . Использование такого профиля ведет к экспоненциальному убыванию отражения при увеличении
.
В случае неполного замощения подложки основаниями пирамидок между этими основаниями имеется зазор (). Вследствие этого согласно имеющимся выражениям для эффективной диэлектрической проницаемости
, то есть в точке
у функции диэлектрической проницаемости
имеется разрыв. Отсюда можно сделать вывод, что при увеличении
отражение выходит на постоянное значение, равное коэффициенту отражения между средами со значениями диэлектрической проницаемости
и
. Мы продемонстрировали это для конусов случае плотной треугольной упаковки.

Коэффициент отражения для различных пирамидок. Сравнение результатов полученных помощью приближения эффективной среды (линии) и FDTD (точки).
Приближение геометрической оптики
Перейдем теперь к рассмотрению оптических свойств текстурированной поверхности в коротковолновом пределе . В этом случае они не зависят от длины волны
и определяются только геометрией задачи.
Ма расчитали отражение для плотно упакованных треугольных и квадратных пирамидок (полное замощение) и конусов (неполное замощение). Результаты, полученные с помощью FDTD находятся в хорошем согласии с результатами, полученными методом трассировки лучей. Расхождение между ними при увеличении связано с тем, что взятое нами в FDTD расчетах значение
в этом случае оказывается недостаточным для того, чтобы работало приближение геометрической оптики.
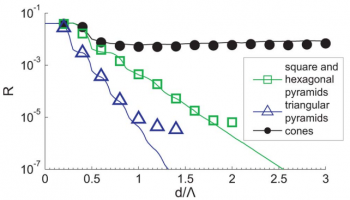
Коэффициент отражения для различных пирамидок. Сравнение результатов метода трассировки лучей (линии) и FDTD (точки).
В случае полного замощения проведенные нами расчеты показали экспоненциальное убывание отражения при увеличении высоты пирамидок. Мы связываем это со следующими соображениями.
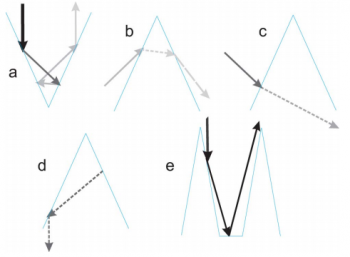
Введем следующую классификацию лучей:
- Падающий луч.
- Отраженные лучи, образованные при отражении падающих от сторон текстуры. Отраженные лучи могут дальше переотражаться. После некоторого числа переотражений
они окончательно отражаются обратно. Угол отражения, амплитуда и фаза таких лучей при каждом отражении могут быть рассчитаны с помощью формул Френеля.
- Преломленные лучи, образованные при прохождении падающих или отраженных лучей в текстуру.
- Вторичные лучи, порожденные преломленными лучами, которым удалось после попадания в текстуру выйти из нее наружу.
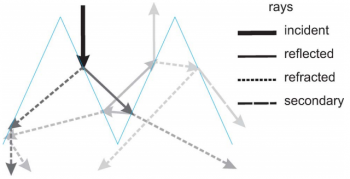
Классификация лучей.
В коэффициент отражения от текстурированной поверхности вносят вклад отраженные и вторичные лучи .
Можно показать, что (a) число переотражений, необходимое падающему лучу, чтобы полностью выйти из структуры, линейно возрастает с увеличением высоты пирамидки. Поскольку после каждого переотражение амплитуда луча умножается на коэффициент отражения от боковой поверхности пирамидки, экспоненциально убывает с ростом высоты пирамидки.
сравним по порядку
по двум соображениям: (b) поскольку
, пирамидка отклоняет выходящие из нее вторичные лучи вниз ближе к нормали, преломленные лучи, после некоторого количества переотражений от внутренней стороны грани пирамидки либо © уходят в подложку, либо (d) достигают угла полного внутреннего отражения, что больше не позволяет им выйти из пирамидки.
В случае неполного замощения (например, плотно упакованные в треугольную решетку конусы) при увеличении отражение вначале падает, а после достижения некоторого минимума поднимается до постоянного значения. Мы связываем это с тем, что (e) при
часть лучей после первоначального отражения от боковой поверхности движется почти параллельно ей и неминуемо попадает в зазор между основаниями, от которого эти лучи окончательно отражаются обратно. В нашем примере плотно упакованных в треугольную решетку конусов это касается практически всех лучей (кроме тех исключительных случаев, когда точка их соударения с боковой поверхностью лежит на плоскости, проходящей через оси соседних конусов), и поэтому при
коэффициент отражения стремится к коэффициенту отражения подложки.
Весь диапазон размеров текстуры
Перейдем теперь к результатам для оптических свойств текстурированной поверхности во всем диапазоне размеров текстуры. Для их получения нами использовался метод FDTD.
Рассмотрим вначале случай полного замощения подложки основаниями пирамидок. Зафиксируем какое-либо значение и исследуем зависимость отражения
от
(см. соответствующие черные кривые на рисунки). При увеличении
от 0 до 1 отражение падает и достигает локального минимума при
, что качественно объясняется тем, эффективная диэлектрическая проницаемость в нулевом приближении не зависит от
, а отражение соответствующего промежуточного слоя падает при увеличении высоты
. При
отражение продолжает падать, проходя ряд локальных минимумов, соответствующих тем значениям
, при которых появляются очередные дифракционные порядки. Отметим, что при
, приближение эффективной среды становится неприменимым, и падение отражения обусловлено эффектами дифракции и интерференции волн, рассеянных на текстурированной поверхности. При больших значениях
размах осцилляций уменьшается, и кривая выходит на предел геометрической оптики.
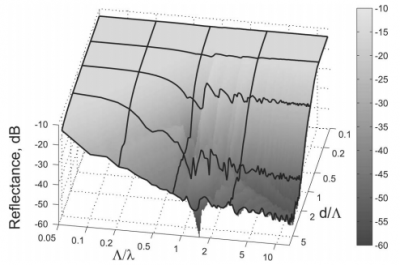
Коэффициент отражения от плотно упакованных квадратных пирамидок. Результаты получены с помощью метода FDTD.
В случае неполного замощения, как, например, для случая плотно упакованных в треугольную решетку конусов, наименьшее значение отражения достигается при порядка длины волны.
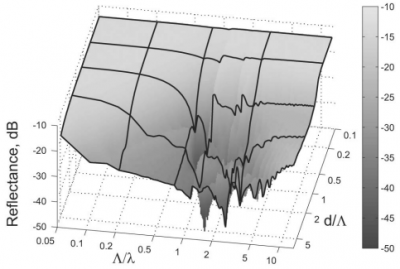
Коэффициент отражения от плотно упакованных треугольную решетку конусов . Результаты получены с помощью метода FDTD.
Итак, нами проведено всестороннее исследование антиотражающих свойств текстурированной поверхности начиная от длинно- и кончая коротковолновым пределами. Для этого использовался метод FDTD, а также приближения эффективной среды и геометрической оптики для длинно- и коротковолнового предельных случаев.
Отимальные размеры текстуры зависят от характера замощения подложки основаниями пирамидок. В случае полного замощения, когда между основаниями нет зазоров, при фиксированной величине отношения наименьшее отражение достигается при
. Это согласуется с тем, что, как мы показали, скорость убывания отражения при росте
и фиксированных
и
в приближении геометрической оптики экспоненциальна, в то время как в приближении эффективной среды она имеет степенной характер. При этом малая величина отражения достижима также и при
порядка длины волны. В случае неполного замощения оптимальное значение
имеет порядок длины волны. Наличие минимума в этом случае также находится в согласии с полученными нами оценками в приближениях эффективной среды и геометрической оптики.
Отметим, что изготовление макротекстурированных поверхностей может являться технологически сложной и материалозатратной задачей. Альтернативой могут служить относительно недорогие современные способы изготовления нанотекстурированных поверхностей, такие как, метод плазменного травления. Вместе с полученным нами результатом достижимости малых значений коэффициента отражения при размерах текстуры порядка длины волны, это служит обоснованием эффективности нанотекстурированных покрытий для оптического диапазона.
Кремниевые текстурированные покрытия
Одним из путей повышения эффективности кремниевого солнечного элемента является применение антиотражающих покрытий. В качестве таковых могут использоваться многослойные покрытия, а также покрытия из пористого кремния, оптические свойства которых подобны свойствам пленки с непрерывно меняющимся показателем преломления, что обусловлено изменением пористости в зависимости от глубины. Однако, обоим этим методам присущи недостатки, обсуждавшиеся нами выше.
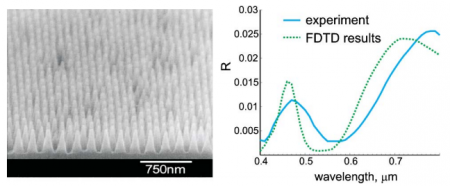
Альтернативным способом уменьшения отражения является применение нанотекстурированных покрытий, интерес к которым особенно возрос в последнее время. В последних имеющихся экспериментальных работах был достигнут коэффициент отражения для нормального падения менее 5% во всем видимом диапазоне (а для некоторых длин волн менее 1%), что соответствует его уменьшению на один - два порядка по сравнению с нетекстурированной поверхностью (коэффициент отражения 30-40%). Для искусственного изготовления текстурированных покрытий могут применяться различные виды литографических техник, голографическое паттернирование фоторезиста с последующим травлением, а также плазменное травление, используемое для получения кремниевых нанотрубок.
Для моделирования кремния в FDTD необходимо учитывать зависимость его диэлектрической проницаемости от длины волны. О том, как это делать, читайте в разделе Фитинг диэлектрической проницаемости.
Ниже мы приводим сравнение экспериментальных данных по отражению от кремниевой текстурированной поверхности и результатов FDTD, взятое отсюда http PDF