Модификация спонтанного излучения
Во многих прикладных задачах моделирования возникает вопрос о модификации спонтанного излучения вблизи нано- или микрообъекта или внутри наноструктурированного образца. Например, это может быть процесс люминесценции или флюоресценции молекулы или супрамолекулярного комплекса в органическом окружении.
В частности, свет, испускаемый органическим светоизлучающим диодом (Organic Light Emitting Diode, OLED, англ.), возникает в результате спонтанного излучения при рекомбинации экситонов, происходящей в излучающем слое OLED’а. Рекомбинация является, по сути, релаксацией электрона с высшего уровня в молекулярном спектре на низший. При этом излучательная рекомбинация определяется дипольным моментом перехода между высшим и низшим уровнями. Темп рекомбинации возбуждения (такого, как экситон) определяется как химическим, так и диэлектрическим окружением возбуждения, и есть сумма двух процессов, а именно, излучательной и безызлучательной релаксации. Диэлектрическое окружение влияет на темп излучательной рекомбинации, который определяется локальной плотностью фотонных состояний (мод), доступных излучателю, а также, на безызлучательную рекомбинацию, а если точнее, поглощение излучения в материале (т.н. омические потери). Последний процесс – это знаменитое металлическое тушение спонтанного излучения, играющее первостепенную роль при изучении спонтанного излучения в материалах. Влияние на безызлучательную рекомбинацию также оказывает химическое окружение излучателя. Моделирование влияния химического окружения происходит на атомистическом уровне. Ниже мы не будем учитывать влияние химического окружения, т.к. это не повлияет на выводы для излучательной рекомбинации и омических потерь.
Принцип соответствия
Принцип соответствия играет ключевую роль в классическом электродинамическом подходе к вычислению темпов рекомбинации. Согласно этому принципу, мощность спонтанного излучения возбужденного состояния излучателя при дипольном переходе соответствует мощности классического электрического диполя с величиной дипольного момента, равной матричному элементу дипольного момента перехода. Темп рекомбинации определяется следующим выражением:
,
где – это мощность,
– частота излучения. То же самое верно и для магнитного дипольного перехода. Здесь предполагается, что и частота, и матричный элемент дипольного перехода практически не зависят от окружения излучателя, что верно в большинстве случаев. Темп излучательной рекомбинации можно получить путем интегрирования дальнего поля излучателя по окружающей его поверхности. Темп безызлучательной рекомбинации получается при интегрировании энергии поля излучения по объему всех поглощающих объектов.
Диполь у поверхности
Впервые принцип соответствия был применен при моделировании спонтанного излучения комплексов Eu3+, помещенных вблизи металлической поверхности. В отличие от предыдущих работ на эту тему, где использовалась механическая модель, метод, описанный в этих исследованиях, позволяет четко разделить излучательную и безызлучательную рекомбинацию. Таким образом, может быть получена информация как о темпах и тех, и других процессов, а также наблюдаемый квантовый выход излучателя в сложном окружении. Наблюдаемый квантовый выход – это отношение числа реальных фотонов, связанных с полем излучения диполя, к числу созданных возбужденных состояний; эта величина отличается от квантового выхода диполя в вакууме, который определяется отношением числа излученных фотонов к числу созданных возбужденных состояний. Когда диполь находится вблизи металлической поверхности, только часть фотонов будет излучена в дальнюю зону, в то время как другая часть поглотится поверхностью. Была изучена зависимость модификации интенсивности люминесценции от расстояния между излучателем и металлом. Кроме того, расчеты проводились для излучателя, находящегося вблизи поглощающего образца конечной толщины, а также между двумя частично отражающими зеркалами. Приведенные примеры расчетов дают наглядное представление о модели, т.к. допускают точное аналитическое решение.
Метод точно предсказывает свойства люминесцирующих молекул около поглощающих поверхностей. В частности, он позволяет описывать безызлучательную рекомбинацию при очень малых расстояниях от поглощающей поверхности.
Диполь вблизи или внутри сферы
Понимание свойств спонтанного излучения излучателей вблизи искривленных поверхностей крайне важно как при разработке OLED’ов, так и в области люминесцентных хемо- и биосенсоров. Полное классическое описание излучения диполя, расположенного вблизи или внутри диэлектрической или проводящей сферы было предложено в пионерских работах Чу и Раппина. Задача со сферой обладает некоторыми интересными нюансами, отсутствующими в случае плоской геометрии, такими как резонансное взаимодействие диполя с частицей при частотах близких к резонансным частотам частицы. Сам метод очень похож на формализм Ми для рассеяния плоской волны на сфере. Падающее (поле диполя) и рассеянное поля раскладываются в ряд по векторным сферическим гармоникам, а на поверхности сферы применяются соответствующие граничные условия. Коэффициентами разложения являются знаменитые коэффициенты Ми. Полученные поля интегрируются в дальней (волновой) зоне по поверхности сферы , заключающей в себе и диполь, и сферу.
Результат вычислений дает информацию о темпе излучательной рекомбинации дипольного источника вблизи или внутри сферы.
В качестве примера модификации и углового перераспределения излучения диполя в сложном диэлектрическом окружении, изучим спектр излучения и угловое распределение диполя, излучающего вблизи металлической сферы. Пусть сфера состоит из серебра и имеет радиус R=80 нм, диполь удален от поверхности сферы на d=20 нм и ориентирован параллельно поверхности. В спектре проявляется сильный максимум на частоте, соответствующей возбуждению локального плазмонного резонанса (рис. Рисунок 1). Угловое распределение излучения при частотах меньше резонансной имеет очень интересную форму, состоящую из пяти горбов (рис. Рисунок 2).
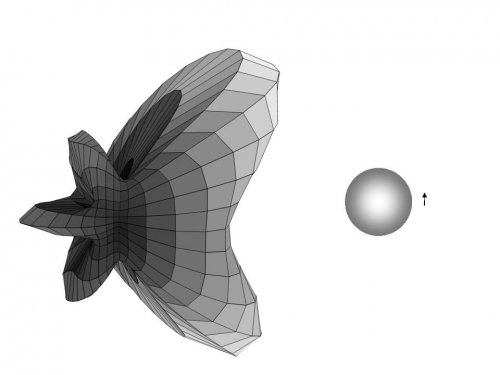
Рисунок 2. Угловое распределение излучения диполя. Справа схематически изображена изучаемая физическая система.
Диполь внутри фотонного кристалла типа лог-пайл
Фотонный кристалл с фотонной запрещенной зоной (Photonic band gap, PBG, англ. Фотонные кристаллы) полностью подавляет излучение источника, находящегося внутри ФК. Мы покажем это на примере вычисления спектра излучения диполя, помещенного внутрь ФК типа лог-пайл. ФК состоит из диэлектрических из упорядоченных в решетку стержней: в каждом слое стрежни параллельны друг другу и расстояние между центрами ближайших соседей – a. Стержни имеют прямоугольное сечение с толщиной w и высотой h. Стержни уложены в слои вдоль оси z. В каждом последующем слое стрежни ориентированы перпендикулярно относительно стрежней в предыдущем слое. Стержни через слой сдвинуты друг относительно друга на a/2. Таким образом, в направлении z период составляет 4 слоя. Вся структура имеет гранецентрированную тетрагональную симметрию. Мы будем рассматривать ФК с такими параметрами: w/a=h/a=0.25 . Материал стержней – GaAs, индекс преломления которого n=3.5. Такой ФК обладает широкой запрещенной зоной в диапазоне частот .
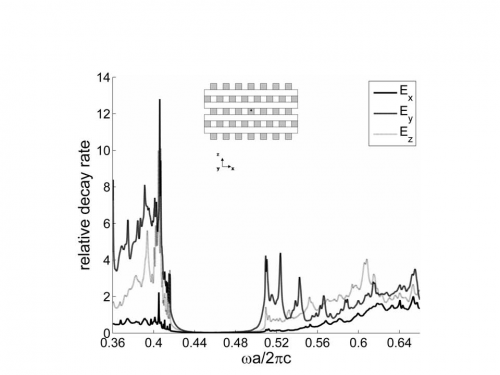
Рисунок 3. Модификация спонтанного излучения в ФК типа лог-пайл.
В области фотонной запрещенной зоны излучения сильно подавлено для всех ориентаций диполя. Значительное усиление на «красном» краю запрещенной зоны в случае z- и y-ориентированного источника связано с краевыми резонансами. Такие резонансы формируются, когда волновой вектор распространяющейся внутри ФК волны находится вблизи края зоны Бриллюэна: групповая скорость волны стремится к нулю, т.е. образуется стоячая волна. Малая групповая скорость соответствует большой плотности состояний, которая проявляется в усилении излучения. Другими словами, усиление является результатом длительного взаимодействия поля с источником вследствие замедления волн вблизи края зоны. Приведенные выше результаты демонстрируют существенную модификацию спонтанного излучения источника, помещенного в ФК на основе полупроводникового материала (GaAs), который является важной компонентой устройств на основе светоизлучающих диодов, таких как экраны, био-сенсоры и лазеры с низким порогом. Использование наноструктурированных полупроводниковых компонент при разработке таких устройств является важным шагом на пути к существенному увеличению их эффективности. Также полученные результаты являются верификацией нашего метода (FDTD) с аналогичными расчетами из литературы.


