Фотонные кристаллы
Фотонные кристаллы (ФК) представляют собой структуры, характеризующиеся периодическим изменением диэлектрической проницаемости в пространстве. Оптические свойства ФК сильно отличаются от оптических свойств сплошных сред. Распространение излучения внутри фотонного кристалла благодаря периодичности среды становится похожим на движение электрона внутри обычного кристалла под действием периодического потенциала. В результате электромагнитные волны в фотонных кристаллах имеют зонный спектр и координатную зависимость, аналогичную блоховским волнам электронов в обычных кристаллах. При определенных условиях в зонной структуре ФК образуются щели, аналогично запрещенным электронным зонам в естественных кристаллах. В зависимости от конкретных свойств (материала элементов, их размера и периода решетки) в спектре ФК могут образовываться как полностью запрещенные по частоте зоны, для которых распространение излучения невозможно независимо от его поляризации и направления, так и частично запрещенные (стоп–зоны), в которых распространение возможно лишь в выделенных направлениях.
Фотонные кристаллы интересны как с фундаментальной точки зрения, так и для многочисленных приложений. На основе фотонных кристаллов создаются и разрабатываются оптические фильтры, волноводы (в частности, в волоконно-оптических линиях связи), устройства, позволяющие осуществлять управление тепловым излучением, на основе фотонных кристаллов были предложены конструкции лазеров с пониженным порогом накачки.
Помимо изменения спектров отражения, прохождения и поглощения металло-диэлектрические фотонные кристаллы обладают специфической плотностью фотонных состояний. Измененная плотность состояний может существенным образом влиять на время жизни возбужденного состояния атома или молекулы, помещенных внутрь фотонного кристалла, и, следовательно, менять характер люминесценции. Например, если частота перехода в молекуле-индикаторе, находящейся в фотонном кристалле, попадет в запрещенную зону, то люминесценция на этой частоте будет подавлена.
ФК делятся на три типа: одномерные, двумерные и трехмерные.
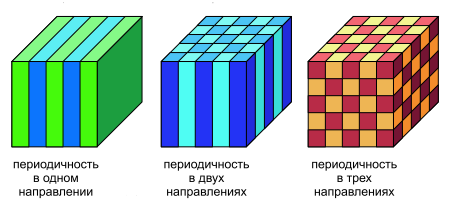
Одно-, двух- и трехмерные фотонные кристаллы. Разные цвета соответствуют материалам с разными значениями диэлектрической проницаемости.
Одномерными являются ФК с чередующимися слоями, сделанными из разных материалов.

Электронный снимок одномерного ФК, используемого в лазере как брэгговское многослойное зеркало.
Двумерные ФК могут иметь более разнообразные геометрии. К ним, например, можно отнести массивы бесконечных по длине цилиндров (их поперечный размер много меньше продольного) или периодические системы цилиндрических отверстий.

Электронные снимки, двумерного прямого и обратного ФК с треугольной решеткой.
Структуры трехмерных ФК весьма разнообразны. Наиболее распространенными в этой категории являются искусственные опалы - упорядоченные системы сферических рассеивателей. Различают два основных типа опалов: прямые и обратные (inverse) опалы. Переход от прямого опала к обратному опалу осуществляется заменой всех сферических элементов полостями (как правило, воздушными), в то время как пространство между этими полостями заполняется каким–либо материалом.
Ниже представлена поверхность ФК, представляющего собой прямой опал с кубической решеткой на основе самоорганизованных сферических микрочастиц полистирола.

Внутренняя поверхность ФК с кубической решеткой на основе самоорганизованных сферических микрочастиц полистирола.
Следующая структура представляет собой инверсный опал, синтезированный в результате многостадийного химического процесса: самосборки полимерных сферических частиц, пропитки пустот полученного материала веществом и удалением полимерной матрицы путем химического травления.

Поверхность кварцевого инверсного опала. Фотография получена с помощью сканирующей электронной микроскопии.
Еще одним типом трехмерных ФК являются структуры типа «поленница» (logpiles), образованные скрещенными, как правило, под прямым углом прямоугольными параллелепипедами.

Электронная фотография ФК из металлических параллелепипедов.
Методы производства
Применение ФК на практике существенно ограничивается отсутствием универсальных и простых методов их изготовления. В наше время реализовано несколько подходов к созданию ФК. Ниже описаны два основных подхода.
Первым из них является так называемый метод самоорганизации или самосборки. При самосборке фотонного кристалла используются коллоидные частицы (самыми распространенными являются монодисперсные кремниевые или полистироловые частицы), которые находятся в жидкости и по мере испарения жидкости осаждаются в объеме. По мере их “осаждения” друг на друга, они формируют трехмерный ФК и упорядочиваются, в зависимости от условий, в кубическую гранецентрированную или гексагональную кристаллическую решетку. Этот метод достаточно медленный, формирование ФК может занять несколько недель. Также к его недостаткам можно отнести плохо контролируемый процент появления дефектов в процессе осаждения.
Одной из разновидностей метода самосборки является так называемый сотовый метод. Этот метод предусматривает фильтрование жидкости, в которой находятся частицы, через малые поры, и позволяет формировать ФК со скоростью, определяемой скоростью течения жидкости через эти поры. По сравнению с обычным методом осаждения указанный способ является гораздо более быстрым, однако и процент появления дефектов при его использовании является более высоким.
К достоинствам описанных методов можно отнести тот факт, что они позволяют формировать образцы ФК больших размеров (площадью до нескольких квадратных сантиметров).
Вторым наиболее популярным методом изготовления ФК является метод травления. Различные методы травления, как правило, применяются для изготовления двумерных ФК. Эти методы основаны на применении маски из фоторезиста (которая задает, например, массив полусфер), сформированной на поверхности диэлектрика или металла и задающей геометрию области травления. Эта маска может быть получена с помощью стандартного метода фотолитографии, за которым непосредственно следует химическое травление поверхности образца с фоторезистом. При этом, соответственно, в областях нахождения фоторезиста, происходит травление поверхности фоторезиста, а в областях без фоторезиста - травление диэлектрика или металла. Процесс продолжается до тех пор, пока не будет достигнута нужная глубина травления, после чего фоторезист смывается.
Недостатком указанного метода является использование процесса фотолитографии, наилучшее пространственное разрешение которой определяется критерием Рэлея. Поэтому этот метод подходит для создания ФК с запрещенной зоной, лежащей, как правило, в ближней инфракрасной области спектра. Чаще всего, для достижения нужного разрешения используется комбинация метода фотолитографии с литографией при помощи электронного пучка. Данный метод является дорогим, но высокоточным методом для изготовления квазидвумерных ФК. В этом методе фоторезист, который меняет свои свойства под действием пучка электронов, облучается в определенных местах для формирования пространственной маски. После облучения часть фоторезиста смывается, а оставшаяся часть используется как маска для травления в последующем технологическом цикле. Максимальное разрешение этого метода составляет порядка 10 нм.
Параллели между электродинамикой и квантовой механикой
Любое решение уравнений Максвелла ,
в случае линейных сред и при отсутствии свободных зарядов и источников тока может быть представлено в виде суперпозиции гармонических во времени функций с комплексными амплитудами
, зависящими от частоты:
Поскольку поля являются вещественными, то , и
можно записать в виде суперпозиции гармонических во времени функций с положительной частотой:
.
Рассмотрение гармонических функций позволяет перейти к частотной форме уравнений Максвелла, не содержащей производных по времени:
,
где временная зависимость участвующих в этих уравнениях полей представляется в виде ,
. Мы предполагаем, что среды изотропны, и магнитная проницаемость
.
Явно выразив поле , взяв ротор от обеих частей уравнений, и подставив второй уравнение в первое, получаем:
,
где – скорость света в пустоте.
Иначе говоря, мы получили задачу на собственные значения:
для оператора
,
где зависимость определяется рассматриваемой структурой.
Собственные функции (моды) полученного оператора должны удовлетворять условию
.
находится как
.
При этом условие соблюдается автоматически, поскольку дивергенция ротора всегда нулю.
Оператор линеен, из чего следует, что любая линейная комбинация решений задачи на собственные значения с той же самой частотой
будет также решением. Можно показать, что в случае
этот оператор эрмитов, т. е. для любых векторных функций
,
где скалярное произведение определяется как
.
Из эрмитовости оператора следует вещественность его собственных значений
. Также можно показать, что при
, собственные значения неотрицательны, а следовательно, частоты
- вещественны.
Скалярное произведение собственных функций, соответствующих разным частотам , всегда равно нулю. В случае равенства частот это не обязательно так, однако всегда можно работать только с ортогональными друг другу линейными комбинациями таких собственных функций. Более того, всегда можно составить базис из собственных ортогональных друг другу функций эрмитова оператора
.
Если, наоборот, выразить поле через
, получается обобщенная задача на собственные значения:
,
в которой операторы присутствуют уже в обеих сторонах уравнения (при этом после деления на оператор в левой части уравнения становится неэрмитовым). В некоторых случаях данная формулировка оказывается удобнее.
Отметим, что при замене в уравнении на собственные значения новому решению
будет соответствовать частота
. Этот факт называется масштабируемостью и имеет большую практическую значимость. Производство фотонных кристаллов с характерными размерами порядка микрона технически сложно. Однако в целях тестирования можно изготовить модель фотонного кристалла с периодом и размером элементов порядка сантиметра, который бы работал в сантиметровом режиме (при этом нужно использовать материалы, которые бы в сантиметровом диапазоне частот обладали примерно такой же диэлектрической проницаемостью, что и моделируемые материалы).
Проведем аналогию описанной выше теории с квантовой механикой.
В квантовой механике рассматривается скалярная волновая функция , принимающая комплексные значения. В электродинамике - векторная, причем комплексная зависимость
вводится лишь для удобства. Следствием этого факта, в частности, является то, что зонные структуры для фотонов в фотонном кристалле будут разными для волн с различной поляризацией в отличие от зонных структур для электронов.
Как в квантовой механике, так и в электродинамике решается задача на собственные значения эрмитового оператора. В квантовой механике эрмитовы операторы соответствуют наблюдаемым величинам.
И наконец, в квантовой механике, если оператор представим в виде суммы
, решение уравнения на собственные значения можно записать как
, то есть задача распадается на три одномерные. В электродинамике это невозможно, поскольку оператор
«связывает» все три координаты, даже если в
они разделяются. По этой причине в электродинамике аналитические решения имеются лишь у весьма ограниченного числа задач. В частности, точные аналитические решения для зонного спектра ФК находятся в основном для одномерных ФК. Именно поэтому важную роль играет численное моделирование для расчета свойств фотонных кристаллов.
Зонная структура
Фотонный кристалл характеризуется периодичностью функции :
,
- проивольный вектор трансляции, представимый в виде
,
где – примитивные вектора трансляции, а
– целые числа.
По теореме Блоха, собственные функции оператора могут быть выбраны таким образом, чтобы они имели форму плоской волны, умноженной на функцию, обладающую той же периодичностью, что и ФК:
,
где - периодичная функция
. При этом значения
можно подбирать таким образом, чтобы они принадлежали первой зоне Бриллюэна.
Подставляя это выражение в сформулированную задачу на собственные значения получаем уравнение на собственные значения
или
,
где
. (1.48)
Собственные функции должны быть периодичны и удовлетворять условию
.
Можно показать, что каждому значению вектора соответствует бесконечный набор мод с дискретным набором частот
, которые мы будем нумеровать в порядке возрастания индексом
.
Поскольку оператор
непрерывно зависит от
, частота
при фиксированном индексе
от
также зависит непрерывно.
Совокупность непрерывных функций
составляют зонную структуру ФК. Изучение зонной структуры ФК позволяет получить информацию о его оптических свойствах.
Наличие какой-либо дополнительной симметрии в ФК позволяет ограничиться некоторой подобластью зоны Бриллюэна, называемой неприводимой. Решения
для
, принадлежащей этой неприводимой зоне, воспроизводят решения для всей зоны Бриллюэна.
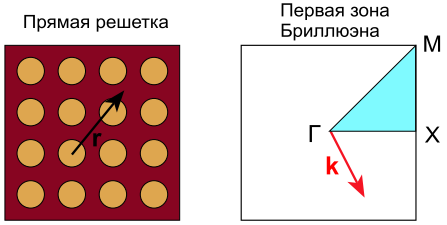
Слева: двумерный фотонный кристалл, состоящий из цилиндров, упакованных в квадратную решетку. Справа: первая зона Бриллюэна, соответствующая квадратной решетке. Голубой треугольник соответствует неприводимой зоне Бриллюэна. Г, М и Х - точки высокой симметрии для квадратной решетки.
Интервалы частот, которым не соответствуют какие-либо моды ни для какого действительного значения волнового вектора, называются запрещенными зонами. Ширина таких зон увеличивается при увеличении контраста диэлектрической проницаемости в ФК (отношение диэлектрических проницаемостей составных элементов фотонного кристалла). Если излучение с частотой, лежащей внутри запрещённой зоны, генерируется внутри такого фотонного кристалла, оно не может распространяться в нём (ему соответствует комплексное значение волнового вектора). Амплитуда такой волны будет экспоненциально затухать внутри кристалла (эванесцентная волна). На этом основано одно из свойств фотонного кристалла: возможность управления спонтанным излучением (в частности, его подавлением). Если же такое излучение падает на ФК извне, то оно полностью отражается от фотонного кристалла. На этом эффекте основано применение ФК для светоотражающих фильтров, а также резонаторов и волноводов с хорошо отражающими стенками.
Как правило, низкочастотные моды концентрируются преимущественно в слоях с большим показателем диэлектрической проницаемости, в то время как высокочастотные по большей части – в слоях с меньшей диэлектрической проницаемостью. Поэтому часто первую зону называют диэлектрической, а следующую за ней - воздушной.
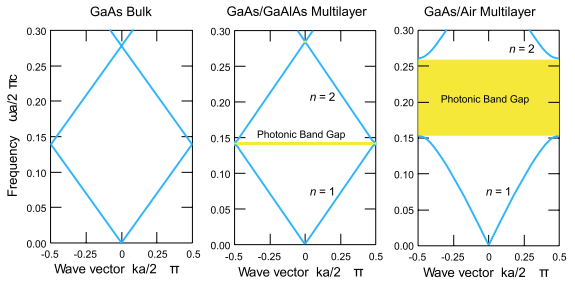
Зонная структура одномерного ФК, соответствующая распространению волны перпендикулярно слоям. Во всех трех случаях каждый слой имеет толщину 0.5a, где a - период ФК. Слева: каждый слой имеет одинаковую диэлектрическую проницаемость ε = 13. По центру: диэлектрическая проницаемость чередующихся слоев имеет значения ε = 12 и ε = 13. Справа: ε = 1 и ε = 13.
В случае ФК с размерностью меньше трех не существует полных запрещенных зон для всех направлений, что является следствием наличия одного или двух направлений, вдоль которых ФК однороден. Интуитивно это можно объяснить тем, что вдоль этих направлений волна не испытывает многократного отражения, требуемого для формирования запрещенных зон.
Несмотря на это, возможно создание одномерных ФК, которые бы отражали волны, падающие на ФК под любыми углами.
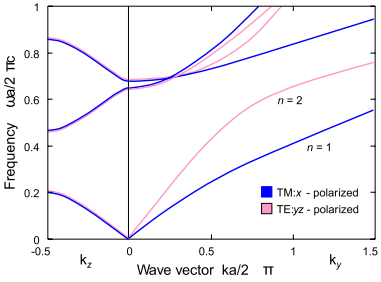
Зонная структура одномерного ФК с периодом a, у которого толщины чередующихся слоев равны 0.2a и 0.8a, а их диэлектрические проницаемости - ε = 13 и ε = 1 соответственно. Левая часть рисунка соответствует направлению распространения волны перпендикулярно слоям (0, 0, kz ), а правая - направлению вдоль слоев (0, ky , 0). Запрещенная зона существует только для направления перпендикулярно слоям. Отметим, что при ky > 0 снимается вырождение для двух различных поляризаций.
Ниже представлена зонная структура ФК, имеющего геометрию опала. Видно, что этот ФК обладает полной запрещенной зоной на длине волны порядка 1.5 мкм и одной стоп-зоной, с максимумом отражения на длине волны 2.5 мкм. Изменяя время травления кремниевой матрицы на одном из этапов изготовления инверсного опала и тем самым, варьируя диаметр сфер, можно добиться локализации запрещенной зоны в определенном диапазоне длин волн. Авторы отмечают, что структура с подобными характеристиками может быть использована в телекоммуникационных технологиях. Излучение на частоте запрещенной зоны может локализоваться внутри объема ФК, а при предоставлении необходимого канала распространяться фактически без потерь. Такой канал может быть сформирован, например, путем удаления элементов фотонного кристалла вдоль некоторой линии. При изгибании канала электромагнитная волна также будет менять направление движения, повторяя форму канала. Таким образом, такой ФК предполагается использовать в качестве передаточного узла между излучающим устройством и оптическим микрочипом, осуществляющим обработку сигнала.
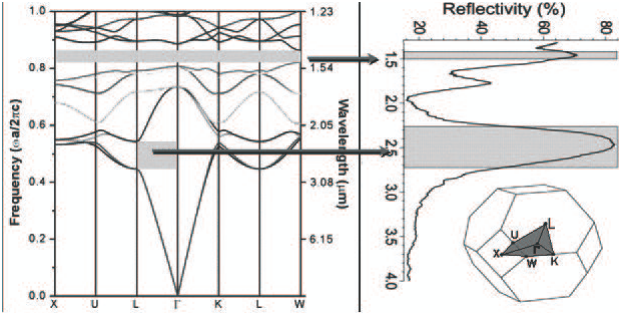
Сравнение спектра отражения в направлении ГL, измеренного экспериментально, и зонной структуры, расчитанной методом разложения по плоским волнам, для инверсного кремниевого (Si) опала с кубической гранецентрированной решеткой (на вкладке изображена первая зона Бриллюэна). Объемная доля кремния 22%. Период решетки 1.23 мкм
В случае одномерных ФК для формирования запрещенной зоны достаточно даже самого малого контраста диэлектрической проницаемости. Казалось бы, для трехмерных диэлектрических ФК можно сделать аналогичный вывод: предположить наличие полной запрещенной зоны при сколь бы то ни было малом контрасте диэлектрической проницаемости в случае, если на границе зоны Бриллюэна вектор имеет одинаковые модули по всем направлениям (что отвечает сферической зоне Бриллюэна). Однако в природе не существует трехмерных кристаллов со сферической зоной Бриллюэна. Как правило, она имеет довольно сложную полигональную форму. Таким образом, получается, что запрещенные зоны по разным направлениям существуют при разных частотах. Только в случае, если диэлектрический контраст является достаточно большим, то стоп-зоны по разным направлениям могут перекрываться и образовывать полную запрещенную зону по всем направлениям. Наиболее близкой к сферической (и таким образом, наиболее независимой от направления блоховского вектора
) является первая зона Бриллюэна гранецентрированной кубической (ГЦК) и алмазной решеток, делая трехмерные ФК с такой структурой наиболее подходящими для формирования полной запрещенной зоны в спектре. При этом, для возникновения полных запрещенных зон в спектрах таких ФК требуется большой контраст диэлектрической проницаемости
. Если обозначить относительную ширину щели как
, то для достижения значений
необходим контраст
для алмазной и
для ГЦК решеток, соответственно. Для использования запрещенных зон в спектрах ФК в различных приложениях необходимо иметь возможность сделать запрещенную зону достаточно широкой, имея ввиду, что все ФК, полученные в экспериментах, неидеальны, а дефекты в структуре могут существенно уменьшить ширину запрещенной зоны.
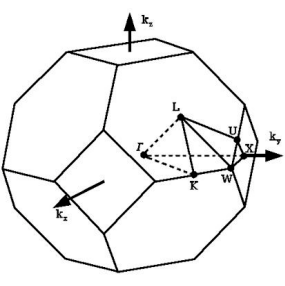
Первая зона Бриллюэна кубической гранецентрированной решетки и точки высокой симметрии.
В заключение еще раз отметим сходство оптических свойств ФК со свойствами электронов в квантовой механикой при рассмотрении зонной структуры твердого тела. Однако при этом между фотонами и электронами имеется существенное различие: электроны обладают сильным взаимодействием между собой. Поэтому «электронные» задачи, как правило, требуют учета многоэлектронных эффектов, сильно увеличивающих размерность задачи, что заставляет часто использовать недостаточно точные приближения, в то время как в ФК, состоящем из элементов с пренебрежимо малым нелинейно-оптическим откликом, данная трудность отсутствует.
Источники света
Перспективным направлением современной оптики является управление излучением с помощью фотонных кристаллов. В частности, в Лаборатории Сандии исследовались ФК типа «поленницы» (log-piles) с целью достижения высокой селективности излучения металлических фотонных кристаллов в ближнем инфракрасном диапазоне, одновременно с сильным подавлением излучения в среднем ИК диапазоне (<20мкм). В этих работах было показано, что для таких ФК излучение в среднем ИК диапазоне сильно подавлено из-за наличия в спектре ФК полной фотонной щели. Однако качество полной фотонной щели падает с ростом температуры из-за увеличения поглощения в вольфраме, что приводит к низкой селективности излучения при высоких температурах.
Согласно закону Кирхгофа для излучения в тепловом равновесии, излучательная способность серого тела (или поверхности) пропорциональна его поглощательной способности. Поэтому для получения информации об излучательной способности металлических ФК можно исследовать их спектры поглощения. Для достижения высокой селективности излучающей структуры в видимом диапазоне ( нм), содержащей ФК, необходимо подобрать такие условия, при которых, поглощение в видимом диапазоне велико, а в ИК - подавлено.
В наших работах httpPDF подробно проанализировано изменение спектра поглощения фотонного кристалла с элементами из вольфрама и с геометрией опала при изменении всех его геометрических параметров: периода решетки, размера вольфрамовых элементов, количества слоев в образце ФК. Проведен также анализ влияния на спектр поглощения дефектов в ФК, возникающих при его изготовлении.


