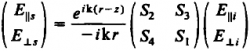Here one can find introductory description of the Finite-Difference Time-Domain (FDTD) method.
FDTD (Finite-Difference Time-Domain)
FDTD is one of the most popular numerical methods in computational electrodynamics. Since introduction in 70th years of the previous century this method became popular due to it certain advantages:
- simplicity of explicit numerical scheme
- high parallel efficiency
- easiness of complex geometry generation
- ability to handle dispersive and nonlinear media
- natural description of impulsive regimes
FDTD includes various numerical techniques and options, such as algorithm for dispersive and nonlinear media modeling, different mesh types, simulation results postprocessing etc.
Real optical applications often require extensive parallel FDTD calculations. One can use existing commercial solutions for this purpose, but they do not provide open code that can be modified. To cover this gap we developed Electromagnetic Template Library.
Yee algorithm
FDTD numerical experiment
Typical scenario of FDTD experiment includes following steps:
- User specifies calculated volume and mesh resolution, optical properties and geometry of the structure, boundary conditions (typically, periodic or absorbing), wave source and set of points where field values should be recorded (we call it detectors).
- Source generates finite time width impulse impinging on structure. Its propagation and scattering is recorded by detectors and possibly transformed to the frequency domain. Total exit of the radiation through absorbing boundaries determines the simulation time.
- Recorded field values are processed (for example, energy flux integrating through the chosen surface) to get optical characteristics of the structure.
Using FDTD
FDTD can be used for varios type of simulations: light scattering from arbitrary shaped objects, modeling of source radiation in specified electromagnetic environment, optical properties of resonators and waveguides. In this section we consider these and other possible examples in details.
Preliminary notes
Solution of Maxwell's equations (
is
or
), in absence of free charges, current sources and any nonlinearities, can be represented as a superposition of harmonic fields:
.
It is convenient to look at as a real part of complex vector
,
where
:
.
Complex dependency is introduced for convenience purposes only and does not have any physical meaning.
The Poynting vector specifies the magnitude and direction of the rate of electromagnetic energy transfer.
The instantaneous Poynting vector is rapidly varying function of time for frequencies that are usually of interest.
Most instruments are not capable of following the rapid oscillations of the instantaneous Poynting vector, but respond to some time average
:
,
where is a time interval long compared with
.
It can be shown that for harmonic field
.
Light intensity is absolute value of
.
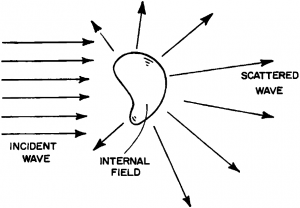
Absorption and scattering by arbitrary object
Consider arbitrary object illuminated by harmonic incident wave. Field in the medium surrounding the object can be represented as superposition of incident and scattered fields:
.
Here we consider how to estimate energy scattered and absorbed by object.
We construct imaginary closed surface around the object ; the net rate at which electromagnetic energy crosses this surface is
,
where is normal to the surface.
If , energy is absorbed within the volume confined by surface.
If object is embedded in nonabsorbing environment,
is the rate at which energy is absorbed by object.
Time averaged Poynting vector can be represented as (we omit here index
for complex vectors
and
)
,
where
.
Last term is a consequence of an interference between incident and scattered fields.
After integrating over surface we have
,
.
For nonabsorbing environment , and
These energy flow rates are linearly dependent on incident wave intensity .
Their normalized values
,
are extinction, absorption and scattering cross sections with dimensions of area.
We may define efficiencies for extinction, scattering and absorption
,
where is the object cross-sectional area projected onto a plane perpendicular to the incident beam (e.g.
for a sphere of radius
).
Particles can scatter and absorb more light that is geometrically incident upon them (corresponding efficiencies are greater than unity) if their sizes are comparable or smaller than the incident wavelength.
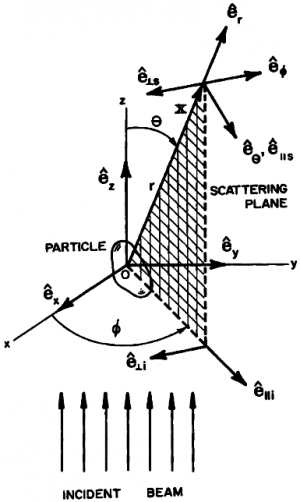
The amplitude scattering matrix
This matrix is used to characterize angular distribution of scattered light.
Consider object that is illuminated by a harmonic wave.
The direction of propagation of the incident light defines axis, the forward direction.
Any point in object may be chosen as the origin
of a rectangular coordinate system, where
and
axes are orthogonal to
axis and to each other but otherwise arbitrary.
The orthonormal basis vectors
,
,
are in direction of positive
,
and
axes.
The scattering direction and forward direction
define a scattering plane.
This plane is uniquely determined by the azimuthal angle
, except when
is parallel to the
axis.
In this two instances (
) any plane containing
axis is a suitable scattering plane.
It is convenient to resolve the incident electric field , which lies in the
plane, into components parallel and perpendicular to the scattering plane
The orthonormal basis vectors
,
form a right-handed triad with :
We also have
,
where ,
,
are orthonormal basis vectors associated with the spherical polar coordinate system
.
If the x and y components of the incident field are denoted by and
, then
,
.
At sufficient distances from the origin (), in the far-field region, the scattered field is approximately transverse (
) and has the asymptotic form
,
where
.
The basis vector is parallel and
is perpendicular to the scattering plane.
Note, however, that
and
are specified relative to different set of basis vectors.
Because of the linearity of Maxwell's equations, the relation between them can be written in matrix form
where (
) are elements of the amplitude scattering matrix, and depend in general on scattering angle
and azimuthal angle
.
Experimental measurement of elements is difficult.
However, the amplitude scattering matrix is related to elements of so called scattering matrix, the measurement of which poses considerable fewer experimental problems.
Scattering matrix is real matrix
, with 7 independent elements, which can be expressed using absolute values
and phase differences between
.
One can find more detailed information in chapter 3.3 of book 1).
Transmission and reflection for planar layers of scatterers
Dipole radiative decay
Applications
EMTL was applied for various range of optical applications. Here is chosen publications list: