Документация
Этот раздел находится в стадии правки.
Проведение эксперимента
Проведение эксперимента FDTD осуществляется посредством класса uiExperiment, объявленного в файле uiexp.h. Нужно создать объект этого класса, а далее последовательно вызывать его функции, с помощью которых задается геометрия эксперимента, проводится расчет и последующий анализ.
Типы данных EMTL
Чтобы разобраться в дальнейшей работе с библиотекой EMTL необходимо немного поговорить про типы данных, используемые в EMTL.
| тип данных | описание | пример |
|---|---|---|
| Vector_2 | Класс для работы с 2-х мерными векторами. В его конструкторе задаются три координаты x, y и z. Вектора можно складывать, вычитать, умножать на число, умножать скалярно (с помощью оператора *) и векторно (с помощью оператора %). | // создаем два вектора v1={1,0} и v2={0,1} Vector_2 v1(1,0),v2(0,1); // v0 = ( {1,0} % {0,1} ) - {0,1} // v0 = ( {0,0} ) - {0,1} = {0,-1} Vector_2 v0=v1%v2 - Vector_2(0,1); // создадим вектор v4 = {1,1} и v5 = {0,0} Vector_2 v4(1), v5(); |
| Vector_3 | Класс для работы с 3-х мерными векторами. В его конструкторе задаются три координаты x, y и z. Вектора можно складывать, вычитать, умножать на число, умножать скалярно (с помощью оператора *) и векторно (с помощью оператора %). | // создаем два вектора v1={1,0,0} и v2={0,1,0} Vector_3 v1(1,0,0),v2(0,1,0); // v0 = ( {1,0,0} % {0,1,0} ) - {0,0,1} // v0 = ( {0,0,1} ) - {0,0,1} = {0,0,0} Vector_3 v0=v1%v2 - Vector_3(0,0,1); // создадим вектор v4 = {1,2,2} и v5 = {0,0,0} Vector_3 v4(1,2), v5(); |
| Plane_3 | Класс, реализующий уравнение плоскости | // Создадим плоскость с нормалью, коллинеарной // оси z и проходящую через начало координат Plane_3 pl(Vector_3(0,0,1), 0); // или Plane_3 pl(Vector_3(0,0,1), Vector_3(0,0,0)); |
| VecContour<2> | Класс - набор 2D точек, описывает 2D контур. | // Единица данных 2D координата Vector_2 value(0,0); // Создадим 2 контура по 10 2D координат VecContour<2> cnt1(10), cnt2(10); // заполним cnt2 значениями {0,0},{0,1},{0,2} и т.д. // (простой перебор) for (int i=0; i < cnt2.GetNPoints(); i++, value[1]++) cnt2.SetPoint(i, value); // добавим в cnt2 еще пару 2D координат в конец // (после этого в cnt2 будет 12 элементов) cnt2.add(Vector_2(0,10)); cnt2.add(Vector_2(0,11)); // выведем содержимое cnt2 for (int j=0; j < cnt2.GetNPoints(); j++) printf("cnt2[%u] (%g,%g)\n" j, (cnt2.GetPoint(j))[0], (cnt2.GetPoint(j))[1]); // заполним cnt1 значениями {0,0},{1,0},{2,0} и т.д. // (перебор элементов происходит через итератор) VecContour<2>::point_iterator it=cnt1.points_begin(), end=cnt1.points_end(); value = Vector_2(0,0); for (; it != end; it++, value[0]++) *it = value; // добавим в cnt1 2D координату в ячейку 14 // (размер cnt1 автоматически увеличится до 14) cnt1.SetPoint(13,Vector_2(13,0)); // выведем содержимое cnt1 // (перебор элементов происходит через итератор) int n=0; for (it = cnt1.points_begin(); it != end; it++, n++) printf("cnt1[%u] (%g,%g)\n" n, (*it)[0], (*it)[1]); |
| VecContour<3> | Класс - набор 3D точек, описывает 3D контур. | // см. пример для VecContour<2>
|
Установка размеров счетной области и граничных условий
Размер счетной области задается в пространственных единицах с помощью функции uiExperiment::SetInternalSpace(). При этом размер сетки для расчета FDTD вычисляется как размер области в пространственных единицах, деленный на шаг сетки в пространственных единицах. Шаг сетки устанавливается функцией uiExperiment::SetResolution(), которой передается значение шаг(ов) по пространственным направлениям, либо функцией uiExperiment::SetResolutionN(), которой передается число шагов по сетке в каждом направлении.
Некоторые данные для расчета в EMTL пакуются, максимально возможный размер памяти в байтах, который может понадобиться для расчета, можно вычислить как полный размер сетки, умноженный на 64 (для версии EMTL с двойной точностью).
При установке размеров счетной области необходимо придерживаться следующих правил:
- В характерную длину волны должно вписываться не менее чем 10-20 временных шагов.
- Размер объекта должен быть не менее чем 2-5 пространственных шагов.
- Фактор Куранта должен быть равен примерно 0.5.
- Размер необходимой для расчета памяти не превышает доступной оперативной памяти.
В EMTL можно задавать периодические (BC_PER), поглощающие(BC_PML) и отражающие (BC_REFL) граничные условия по каждой из осей.
Пример:
int main(int argc, char **argv){ emInit(argc,argv); // инициализируем библиотеку EMTL uiExperiment task; // создадим экземпляр класса, через который будем управлять экспериментом // установим размеры счетной области в пространственных единицах 20 х 20 х 20 task.SetInternalSpace(Vector_3(-10,-10,-10), Vector_3(10,10,10)); // установим шаг сетки равным 0.25 и фактор Куранта равным 0.5 task.SetResolution(0.25,0.5); // в таком случае размер сетки будет равен 20/0.25 х 20/0.25 х 20/0.25 или 80 х 80 х 80 ячеек, // максимальный размер памяти, необходимой для расчета будет равен 80^3 * 64 = 32 768 000 байт. // временной шаг вычисляется как фактор_Куранта * шаг_сетки и будет равен 0.25 * 0.5 или 0.125. // установить периодические условия для осей X и Y и поглощающие по оси Z task.SetBC (BC_PER, BC_PER, BC_PML); ... // остальной код программы return 0; }(найти описание функции emInit() и классов uiExperiment и Vector_3 можно тут и тут)
Параметры среды и материалов
За параметры среды и материалов отвечает класс emMedium. В его конструктор передаются диэлектрическая проницаемость , электропроводность
, магнитная проницаемость
и магнитные потери
. По умолчанию их значения равны 1, 0, 1, 0.
... task.SetFillMedium(emMedium(2,0,1,0)); // установить параметры среды с диэлектрической проницаемостью = 2, // электропроводностью = 0, магнитной проницаемостью = 1, и магнитными потерями = 0 ...
EMTL не предполагает возможности табличного задания зависимости диэлектрической проницаемости от частоты. Однако в EMTL можно задать эту зависимость в виде произвольного числа членов в форме Друде и Лоренца:
Например, золото можно задать следующим образом
emMedium m(5.4); m.AddPolarizability(emDrude(.14*1e17,.103*1e+15/2,1)); m.AddPolarizability(emLorentz(.427*1e+16,.87*1e+15,2.54*.268)); m.AddPolarizability(emLorentz(.523*1e+16,1.32*1e+15,2.54*.732)); m.calibrate(1/(299792458*1e+6));
Параметры конструкторов для членов Друде и Лоренца такие: плазменная частота и затухание
и величина
. Конкретные данные для золота взяты из работы [http://www.opticsinfobase.org/oe/abstract.cfm?uri=OE-15-26-18119].
Задаваемая плазменная частота и затухание
должны измеряться в радианах на единицу измерения времени EMTL. В данном примере изначальные данные для золота имеют размерность радиан / секунду. Если единицей измерения длины EMTL является микрон, то, соответственно, единицей измерения времени EMTL является время, за которое свет проходит один микрон. Для того, чтобы придать значениям
,
требуемую размерность, мы воспользовались функцией calibrate, которая умножает
и
(а также
и
) на свой аргумент (в данном случае на обратную скорость света, сек/мкм).
В случаях, когда у Вас имеется табличная зависимость диэлектрической проницаемости среды от частоты, ее необходимо аппроксимировать с помощью произвольного числа членов Друде, Лоренца. Для некоторых часто используемых сред (золото, серебро, кремний, вольфрам и т. д.) такая аппроксимация в EMTL уже есть. Для того, чтобы ей воспользоваться, нужно вызвать подходящую функцию, возвращающую объект emMedium.
double s = 1; // единица длины в EMTL, по умолчанию считается, что она равна 1 микрону emMedium glass = getGlass(); // параметры среды для стекла emMedium polysterene = getPolysterene(); // параметры среды для полистерена emMedium w_298 = getW_298(s); // параметры среды для фольфрама при температуре 298 К emMedium w_2400 = getW_2400(s); // параметры среды для фольфрама при температуре 2400 К emMedium au = getAu(s); // параметры среды для золота emMedium ag = getAg(s); // параметры среды для серебра emMedium si = getSi(s); // параметры среды для кристаллического кремния emMedium asi = getaSi(s); // параметры среды для аморфного кремния
Геометрические тела
В EMTL есть двухмерные тела (это многоугольник и круг) и разнообразные выпуклые трехмерные тела, подробнее о которых написано ниже.
Тела необходимо в начале создать из соответствующих классов, а затем добавить их на сетку вызвав функцию AddObject класса uiExperiment. Визуализировать можно только тела, добавленные на сетку. При добавлении тела на сетку нужно указать, должен ли класс uiExperiment сам освобождать память, выделенную под тело (параметр 3 функции AddObject, 1 -надо, 0 -не надо) и можно указать его Level (уровень), по умолчанию равный 0. Level отвечает за приоритет применения того или иного тела при расчете. Чем Level больше, тем больше приоритет. Это нужно для того, чтобы вырезать одно тело из другого или создать невыпуклое тело. При этом существует ограничение: если тела пересекаются, тогда одно тело должно полностью лежать на другом теле. Более подробное описание и примеры построения невыпуклых объектов ищите ниже.
Координаты двухмерных тел указываются относительно некоторой начальной точки построения 2D фигуры. Координаты трехмерных тел указываются сразу в координатах счетной области.
При выполнении функции BuildGeometry() EMTL генерирует файлы с получившейся геометрией эксперимента (визуализацией), которые можно посмотреть с помощью программ gnuplot или paraview. Подробнее о визуализации смотрите в соответствующих разделах.
#include "uiexp.h" int main(int argc, char **argv){ emInit(argc,argv); // инициализируем библиотеку EMTL uiExperiment task; // создадим экземпляр класса, через который будем управлять экспериментом task.SetFillMedium(emMedium(2,0,1,0)); // установить параметры среды task.SetInternalSpace(Vector_3(-10,-10,-10), Vector_3(10,10,10)); // установим размеры task.SetResolution(0.25,0.5); // установим разрешение и фактор Куранта Sphere sph(2, Vector_3(0,0,0) ); // создадим тело сферу радиусом 2 с центром в точке {0,0,0} task.AddObject(emMedium(1.45),&sph,0,0);// поместим созданный объект в счетную область указав // для него параметры среды (диэл.прониц.), managed=0 (не // пытаться удалить sph автоматически) и level=0(его уровень) task.BuildGeometry(); // построить геометрию эксперимента, чтобы EMTL сгенерировал файлы с геометрией // теперь можно посмотреть что получилось с помощью gnuplot или paraview ... // остальной код программы return 0; }
Далее будут подробно рассмотрены способы создания различных геометрических объектов и примеры работы с ними.
2D тела
Многоугольник (Polygon_2)
Многоугольник - это двухмерная фигура, которая создается на основе набора 2D координат (контура).
VecContour<2> cnt; // создадим пустой набор точек (пустой контур) // Добавим 4 2D координаты {0,0}, {0,1}, {1,0}, {1,1} cnt.add(Vector_2(0,0)); cnt.add(Vector_2(0,1)); cnt.add(Vector_2(1,0)); cnt.add(Vector_2(1,1)); // Создадим на его основе многоугольник Polygon_2 poly(&cnt); // Получим обратно из многоугольника набор 2D координат (контур) cnt = *( poly->get_contour() );
Круг (Circle)
Круг - это двухмерная фигура, которая задается радиусом R и координатами центра.
// создать круг с радиусом 2 и центром в точке с координатами 0,0 Circle cir(2, Vector_2(0,0));
3D тела
В EMTL есть несколько способов создать выпуклый трехмерный объект - с помощью простых примитивов (сфера, прямоугольный параллелепипед), сложных примитивов (бесконечные цилиндр и конус с произвольной двухмерной фигурой в основании) и с помощью многогранников, заданных произвольным числом плоскостей.
Любой примитив можно перевести в многогранник или ограничить плоскостями. Тела, состоящие из многогранников, можно наклонять или вращать.
При этом, если тела выходят за границы вычислительного объема, то рассматривается только та их часть, которая в него попадает.
Создание простых примитивов
К простым примитивам относятся Сфера и Прямоугольный параллелепипед, ребра которого параллельны координатным осям. Сфера задается радиусом и координатой центра. Прямоугольный параллелепипед задается указанием координат его левого нижнего и правого верхнего углов.
// Создадим сферу радиусом 2 с центром в точке с координатами 0,0,0 Sphere sph(2, Vector_3(0,0,0) ); // Создадим прямоугольный параллелепипед с левым нижним углом, // находящимся в точке с координатами -1,-1,-1 и правым верхним углом, // находящимся в точке с координатами 1,1,1. Box box( Vector_3(-1,-1,-1), Vector_3(1,1,1) );
Создание сложных примитивов
К сложным примитивам относятся бесконечные цилиндр и конус с произвольной двухмерной фигурой в основании (кругом или многоугольником). Они представляют собой шаблоны классов, параметром которых является класс, описывающий эту 2D фигуру. (Например Cylinder < Circle > - Бесконечный цилиндр с основанием Круг. Тогда создание такого объекта будет выглядеть следующим образом: Cylinder <Circle> cyl = Cylinder <Circle> (origin, n, x, y, &cir) где cir - уже созданный объект класса Circle)
Цилиндр описывается 3D координатой, в которую помещается начальная точка построения 2D фигуры и через которую проходит плоскость, в которой эта 2D фигура лежит, 3D вектором направления оси цилиндра, 3D векторами, которые указывают направления x и y осей для 2D фигуры (и характеризуют собой плоскость, в которой лежит эта 2D фигура), а также самой фигурой в основании. Конус описывается так же, только вектор направления оси конуса также отвечает за его высоту (вершину конуса).
Сейчас существует ограничение, направление оси 3D фигуры и направления 3D осей x и y для 2D фигуры должны бить взаимно ортогональны.
Чтобы получить конечный цилиндр с основанием круг, существует готовая глобальная функция GetCylinder. Так же можно ограничить бесконечный цилиндр вручную набором плоскостей получив новый 3D объект ConfinedRegion. О том как это сделать, читайте ниже. Если вручную ограничивать бесконечный цилиндр плоскостями, можно получить например наклоненный конечный цилиндр.
// Зададим различные параметры Vector_3 origin (0,0,0), n (0,0,1), l (0,0,2), x (1,0,0), y (0,1,0); double r = 2, h = 3; // Круг, с радиусом 2 и координатами 0,0,0 Circle cir (r, Vector_2(0,0) ); // Создание бесконечного цилиндра с основанием Круг, ось цилиндра // проходит через точку origin и направлена вдоль оси Z, // Оси x и y 2D плоскости, в которой лежит основание (круг), // направлены вдоль осей x и y трехмерного пространства. // (Ограничение соблюдается - вектора n, x и y - взаимно ортогональны.) Cylinder<Circle> cyl(origin, n, x, y, &cir); // Создание бесконечного конуса аналогично. Высота конуса будет равна 2. // Таким образом вершина конуса будет находится в точке 0,0,2 Cone<Circle> con(origin, l, x, y, &cir); // Создать конечный цилиндр радиусом r=2, высотой h=3, // с началом в точке origin={0,0,0} и с осью коллинеарной вектору n={0,0,1} ConfinedRegion<Cylinder<Circle> > * cyl2 = GetCylinder(origin, n, r, h);
Создание многогранников
С помощью многогранников можно с некоторой приближенностью описать любое выпуклое тело. Многогранник создается на основе набора плоскостей. Если плоскости в каком либо направлении не ограничивают фигуру, она считается бесконечной в этом направлении (на деле обрезается на краю счетной области).
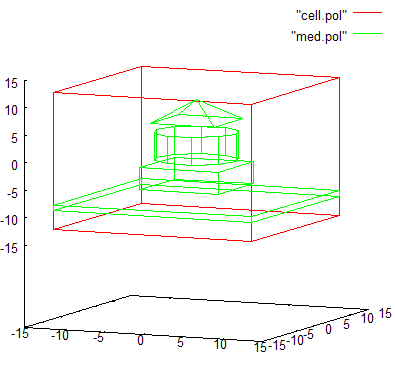
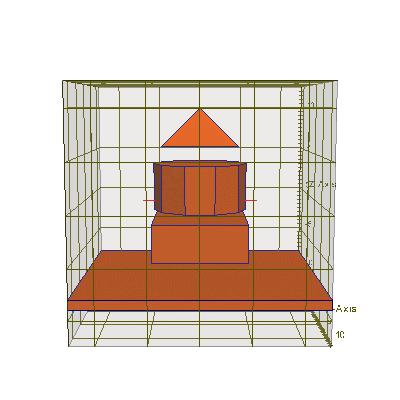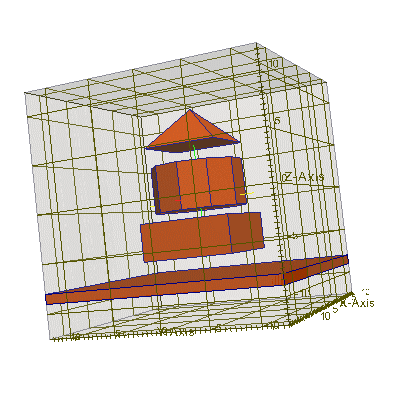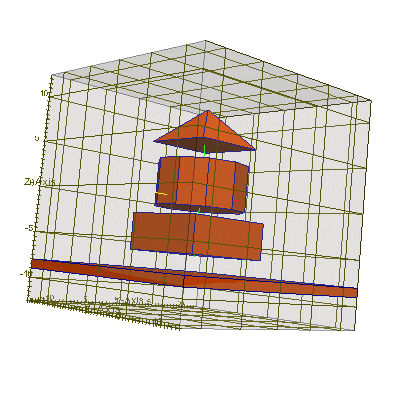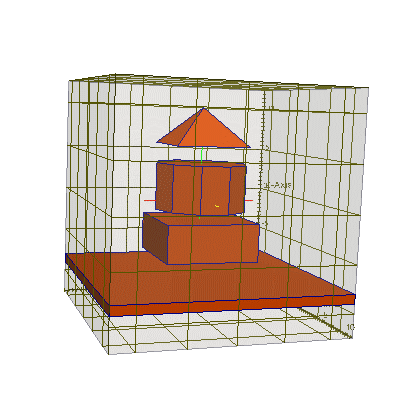
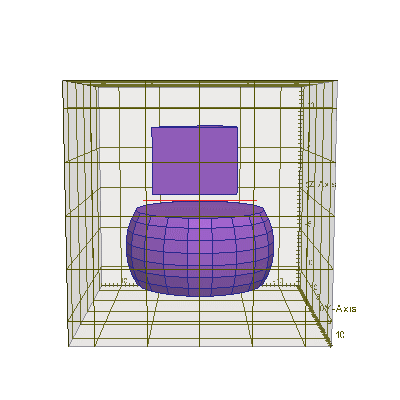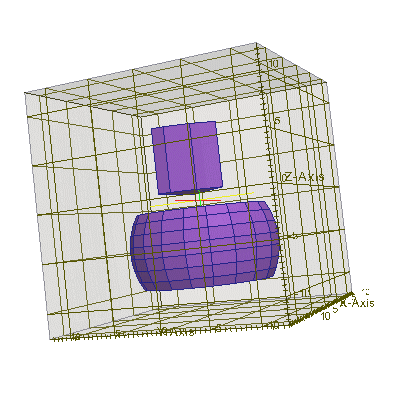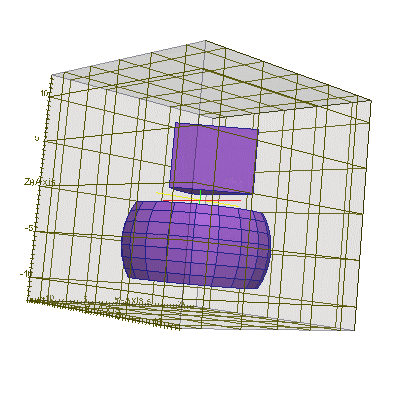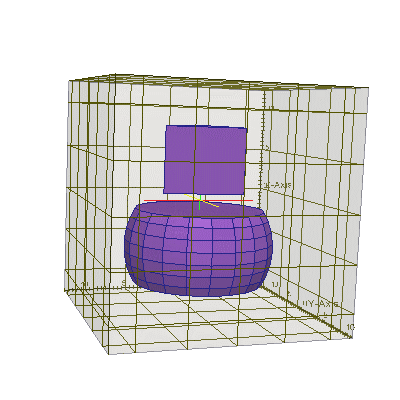
#include "uiexp.h" int main(int argc,char **argv){ emInit(argc,argv); // инициализация библиотеки EMTL uiExperiment task; // создание эксперимента task.SetInternalSpace(Vector_3(-10,-10,-10), Vector_3(10,10,10)); // размеры // Создать прямоугольный параллелепипед Plane_3 * box_planes = new Plane_3[6]; // создать набор из 6 плоскостей box_planes[0].init ( Vector_3(0,0,1), Vector_3(0,0,-6) ); // низ box_planes[1].init ( Vector_3(0,0,-1), Vector_3(0,0,-2) ); // верх box_planes[2].init ( Vector_3(0,1,0), Vector_3(0,-5,0) ); // сторона 1 box_planes[3].init ( Vector_3(0,-1,0), Vector_3(0,5,0) ); // сторона 2 box_planes[4].init ( Vector_3(1,0,0), Vector_3(-5,0,0) ); // сторона 3 box_planes[5].init ( Vector_3(-1,0,0), Vector_3(5,0,0) ); // сторона 4 Polyhedron_3 box_poly(box_planes, box_planes+6);// создать на основе плоскостей тело task.AddObject(emMedium(1.45), &box_poly, 0); // поместить это тело на сетку // Создать бесконечную пластинку Plane_3 * pl_planes = new Plane_3[2]; // создать набор из 2 плоскостей pl_planes[0].init ( Vector_3(0,0,1), Vector_3(0,0,-9) ); // низ пластинки pl_planes[1].init ( Vector_3(0,0,-1), Vector_3(0,0,-8) ); // верх пластинки Polyhedron_3 pl_poly (pl_planes, pl_planes+2); // создать на основе плоскостей тело task.AddObject(emMedium(1.45), &pl_poly, 0); // поместить это тело на сетку // Создать пирамиду Plane_3 * pir_planes = new Plane_3[5]; // создать набор из 5 плоскостей pir_planes[0].init ( Vector_3(0,0,1), Vector_3(0,0,6) ); // низ pir_planes[1].init ( Vector_3(0,1,-1), Vector_3(0,-4,6)); // верх pir_planes[2].init ( Vector_3(0,-1,-1),Vector_3(0,4,6) ); // верх pir_planes[3].init ( Vector_3(1,0,-1), Vector_3(-4,0,6)); // верх pir_planes[4].init ( Vector_3(-1,0,-1),Vector_3(4,0,6) ); // верх Polyhedron_3 pir_poly(pir_planes, pir_planes+5);// создать на основе плоскостей тело task.AddObject(emMedium(1.45), &pir_poly, 0); // поместить это тело на сетку // Создать цилиндр с помощью плоскостей (более сложный пример) double r = 5, h = 5; // радиус цилиндра и его высота int n_points = 10; // количество углов в окружности цилиндра Vector_3 origin (0,0,-1), // координаты точки в середине основания цилиндра x (1,0,0), y (0,1,0), n (0,0,1); // x и y для 2D основания и вектор оси цилиндра VecContour<2> cnt; // создать пустой контур (набор 2D точек) for (int i=0; i<n_points; i++) { // заполнить этот контур (набор 2D точек) double fi = 2*M_PI*double(i)/double(n_points); cnt.add( Vector_2(r*cos(fi),r*sin(fi)) ); } Plane_3 * planes = new Plane_3[n_points+2]; // создать набор плоскостей (+верх и +низ) // перебрать через итератор все точки контура cnt и заполнить набор плоскостей planes VecContour<2>::point_iterator it=cnt.points_begin(), e=cnt.points_end(); Vector_2 v2=*it; // получить первую 2D координату контура Vector_3 b0 = origin+v2[0]*x+v2[1]*y+n; // перенести её в 3D пространство Vector_3 b1=b0; // запомнить эту первую 2D координату контура ++it; // перейти ко второй 2D координате контура for (int i=0; it!=e; ++it, i++) { // так же перебирать все оставшиеся 2D координаты Vector_2 v2=*it; // получить следующую 2D координату контура Vector_3 b2=origin+v2[0]*x+v2[1]*y+n; // перенести ее в 3D пространство Vector_3 n1=-(b2-b1)%(n); // получить нормаль для очередной боковой плоскости // (% - это векторное перемножение) planes[i].init(n1,b1); // создать очередную боковую плоскость // с нормалью n и точкой основания b1 b1=b2; // сохранить текущую 3D точку } Vector_3 n2=-(b0-b1)%(n); // получить нормаль для последней боковой плоскости planes[n_points-1].init(n2,b1); // создать последнюю боковую плоскость planes[n_points ].init(n,origin); // создать нижнюю плоскость planes[n_points+1].init(-n,origin + h*n); // создать верхнюю плоскость // создать тело, образованное набором плоскостей Polyhedron_3 cyl_poly (planes, planes+n_points+2); task.AddObject(emMedium(1.45), &cyl_poly, 0); // поместить это тело на сетку task.BuildGeometry(); // построить геометрию эксперимента, чтобы EMTL сгенерировал // файлы с геометрией для gnuplot и paraview (результат см.ниже) }
Ограничение тел плоскостями
В EMTL существует класс ConfinedRegion, предназначенный для создания тела, являющегося результатом пересечения любого выпуклого геометрического тела с многогранником Polyhedron_3. Его можно использовать, например, для отсечения части сферы, цилиндра или конуса. Класс ConfinedRegion является шаблонным классом, аргументом которого является класс отвечающий за трехмерное геометрическое тело (это может быть даже сам ConfinedRegion). Для примера функция GetCylinder в качестве конечного цилиндра возвращает как раз объект класса ConfinedRegion.
... // создать тело - сферу, ограниченную сверху и снизу 2-мя плоскостями Sphere sph (8, Vector_3(0,0,-5)); // создать сферу Plane_3 *sph_planes = new Plane_3[2]; // создать набор из 2-х плоскостей sph_planes[0] = Plane_3( Vector_3(0,0,1), Vector_3(0,0,-9) ); sph_planes[1] = Plane_3( Vector_3(0,0,-1),Vector_3(0,0,-1) ); Polyhedron_3 sph_poly (sph_planes, sph_planes+2); // создать бесконечную пластинку ConfinedRegion <Sphere> sph_region (&sph, &sph_poly); // создать тело - пересечение task.AddObject(emMedium(1.45), &sph_region, 0); // поместить его на сетку // создать тело - клинышек, состоящий из бесконечного цилиндра, ограниченного многогранником Cylinder<Circle> * cyl = GetCylinder (Vector_3(5,3,2), Vector_3(0,0,1), 9); //беск. цилиндр Plane_3 *cyl_planes = new Plane_3[4]; // создать набор из 4-х плоскостей cyl_planes[0] = Plane_3( Vector_3(0,-1,0), Vector_3(5,3,0) ); cyl_planes[1] = Plane_3( Vector_3(-1,1,0), Vector_3(5,3,0) ); cyl_planes[2] = Plane_3( Vector_3(0,0,-1), Vector_3(5,3,8) ); cyl_planes[3] = Plane_3( Vector_3(0,0, 1), Vector_3(5,3,1) ); Polyhedron_3 cyl_poly (cyl_planes, cyl_planes+4); // создать многогранник ConfinedRegion <Cylinder<Circle> > cyl_region ( cyl, &cyl_poly );//созд. тело - пересечение task.AddObject(emMedium(1.45), &cyl_region, 0); ...
Создание невыпуклых тел
Невыпуклые тела создаются путем наложения одних выпуклых тел на другие. При этом существует ограничение: если тела пересекаются, тогда одно тело должно полностью лежать на другом теле.
Для того чтобы создать невыпуклое тело, необходимо на выпуклое тело с некоторыми параметрами материала наложить, там где это необходимо, тела с параметрами материала, совпадающими с параметрами среды. При этом у тела, которое накладывается, значение Level (уровня) должно быть выше, чем у тела, на которое оно накладывается.
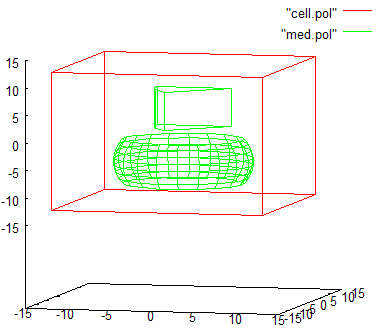
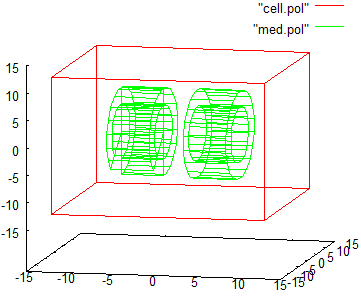
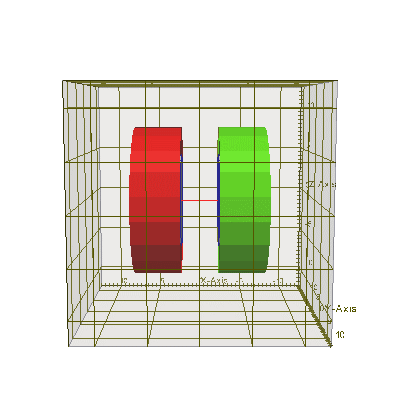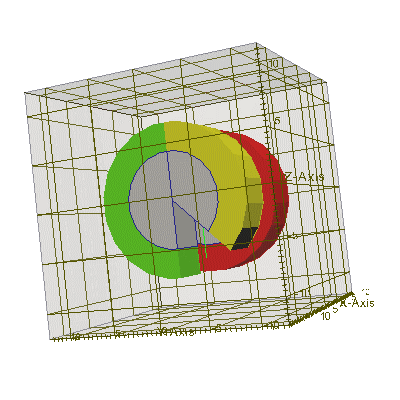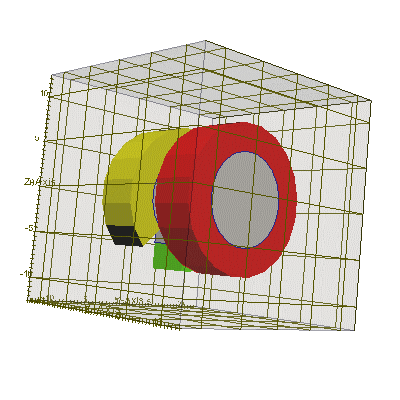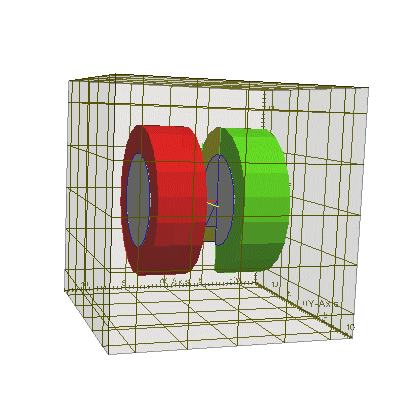
// пример создания колечка и колечка с прорезью #include "uiexp.h" int main(int argc, char **argv){ emInit(argc,argv); // инициализируем библиотеку EMTL uiExperiment task; // создание эксперимента task.SetInternalSpace(Vector_3(-10,-10,-10), Vector_3(10,10,10)); // установим размеры task.SetResolution(0.25,0.5); // установим разрешение и фактор Куранта task.SetFillMedium(emMedium(1)); // задать параметры среды // создать колечко // создать два тела - цилиндра. ConfinedRegion<Cylinder<Circle> > * cyl1 = GetCylinder (Vector_3(2,0,0), Vector_3(1,0,0), 8, 5); ConfinedRegion<Cylinder<Circle> > * cyl2 = GetCylinder (Vector_3(2,0,0), Vector_3(1,0,0), 5, 5); //поместить в счетную область основное тело с необходимыми параметрами материала и Level = 0 task.AddObject(getAu(0.1), cyl1, 1, 0); // укажем, что EMTL сама должна удалить в конце cyl1 //поместить в счетную область накладываемое тело с параметрами материала //равными параметрам среды и со значением Level = 1 task.AddObject(emMedium(1), cyl2, 1, 1); // укажем, что EMTL сама должна удалить в конце cyl2 // создать колчеко с прорезью // для этого содадим 4 выпуклых сегмента цилиндра и попарно наложим их друг на друга // создать два тела - бесконечных цилиндра (для создания с ними 4 тел-пересечений) Cylinder<Circle> * cyli1 = GetCylinder (Vector_3(-7,0,0), Vector_3(1,0,0), 8); Cylinder<Circle> * cyli2 = GetCylinder (Vector_3(-7,0,0), Vector_3(1,0,0), 5); // создать один многогранник для пересечения с бесконечными цилиндрами Plane_3 *cyl1_planes = new Plane_3[4]; // создать набор из 4-х плоскостей cyl1_planes[0].init( Vector_3( 1,0,0), Vector_3(-7,0,0) );// верх cyl1_planes[1].init( Vector_3(-1,0,0), Vector_3(-2,0,0) );// низ cyl1_planes[2].init( Vector_3(0,-1,0), Vector_3( 0,0,0) );// ребро cyl1_planes[3].init( Vector_3(0,-1,1), Vector_3( 0,0,0) );// ребро Polyhedron_3 cyl1_poly (cyl1_planes, cyl1_planes+4); // создать сам многогранник // создать второй многогранник для пересечения с бесконечными цилиндрами Plane_3 *cyl2_planes = new Plane_3[4]; // создать набор из 4-х плоскостей cyl2_planes[0].init( Vector_3( 1,0,0), Vector_3(-7,0,0) );// верх cyl2_planes[1].init( Vector_3(-1,0,0), Vector_3(-2,0,0) );// низ cyl2_planes[2].init( Vector_3( 0,1,0), Vector_3( 0,0,0) );// ребро Polyhedron_3 cyl2_poly (cyl2_planes, cyl2_planes+3); // создать сам многогранник ConfinedRegion <Cylinder<Circle> > cyl11_region ( cyli1, &cyl1_poly );//созд. тело - пересечение ConfinedRegion <Cylinder<Circle> > cyl12_region ( cyli2, &cyl1_poly );//созд. тело - пересечение ConfinedRegion <Cylinder<Circle> > cyl21_region ( cyli1, &cyl2_poly );//созд. тело - пересечение ConfinedRegion <Cylinder<Circle> > cyl22_region ( cyli2, &cyl2_poly );//созд. тело - пересечение task.AddObject(getAu(0.1), &cyl11_region, 0, 0); // один сегмент колечка task.AddObject(emMedium(1), &cyl12_region, 0, 1); // вырежем из него сердцевину task.AddObject(getAu(0.1), &cyl21_region, 0, 0); // второй сегмент колечка task.AddObject(emMedium(1), &cyl22_region, 0, 1); // также вырежем из него сердцевину task.BuildGeometry(); // построить геометрию эксперимента, чтобы EMTL сгенерировал // файлы с геометрией для gnuplot и paraview (результат см.ниже) return 0; }
Источники
В EMTL есть несколько типов источников излучения и технологий работы с ними. Также есть несколько временнЫх форм сигнала, характеризующих излучение от источников, и есть возможность создавать свои собственные временнЫе формы.
При этом в EMTL существуют понятия «источник излучения» и «набор источников излучения». Если в эксперименте необходимо работать только с одним типом источника и одной технологией его работы, то можно не вникать в разницу между «набором источников» и «источником», а также в подробности работы с ними. Можно просто выбрать из примеров, приведенных ниже тот, который Вам подходит и считать что везде речь идет просто об источнике излучения.
Но если необходимо работать с несколькими источниками излучения, работающими по разной технологии или требующими для себя разных временных форм, то разбираться в подробностях работы с наборами источников придется.
В EMTL любой источник должен находиться в составе набора. При этом каждый набор должен состоять только из источников, работающих по одной и той же технологии. Конечные свойства источника складываются из его собственных свойств (например координат) и свойств набора (например временнАя форма сигнала). В начале работы по умолчанию сразу создаются два набора для источников, работающих по двум технологиям, поддерживаемым в EMTL. В них соответственно автоматически добавляются источники, если при их создании не указывается иное.
В настоящее время в EMTL реализованы две технологии работы с источниками, это:
- TF/SF (Total Field /Scattered Field) - корректировка полей на генерирующей поверхности по аналитической формуле. Все источники, работающие по этой технологии далее будут называться TF/SF источниками;
- Модификация
в уравнениях Максвелла для заданных ячеек. Все источники, работающие по этой технологии далее будут называться внутренними источниками тока.
При этом из TF/SF источников в EMTL в данный момент может быть создан только один набор, в который можно добавить одну плоскую TF/SF волну или один или несколько точечных TF/SF источников излучения.
Из внутренних источников тока в EMTL можно создавать несколько наборов точечных источников.
Перед тем как добавлять в эксперимент различные источники излучения необходимо определиться с временными формами сигналов добавив их в эксперимент. Можно добавить одну временную форму сигнала по умолчанию или добавить несколько временных форм сигналов, а затем связать их с наборами источников. Если ни одна временная форма сигнала не задана, EMTL устанавливает по умолчанию форму Беренгера с параметрами, основанными на размерах объектов и размерах счетной области.
Как в EMTL создавать свои временные формы сигналов будет рассказано позже.
Источники с использованием технологии TF/SF.
Технология TFSF состоит в разбиении пространства на область полного поля (это область, по которой проходит волна от источника) и область рассеянного поля (здесь волны от источника нет и поэтому остаются только отраженные и рассеянные волны). На границе этих областей на каждом шаге по времени модифицируются поля E и Н по аналитической формуле. Эта аналитическая формула соответствует распространению волны определенного типа (плоской волны либо волны от точечного источника (диполя)). Где какая область определяется для каждого источника отдельно и зависит от направления волны, которую он генерирует. Волна от источника добавляется (как бы появляется) на границе областей TFSF и на следующей границе областей TFSF отнимается (исчезает). Та область, по которой она проходит, и называется областью полного поля.
В EMTL можно задать только одну границу областей TF/SF, так как граница областей TF/SF задается сразу для всего набора TF/SF источников, а набор таких источников в EMTL можно создать только один. Так же и с формой временного сигнала. При этом и для плоской TFSF волны, и для каждого точечного TFSF источника можно указывать индивидуальные множитель амплитуды и временной сдвиг для установленной на весь набор формы временного сигнала.
Поэтому если необходимо работать только с источниками TF/SF, можно опять таки не вникать в подробности работы с наборами источников, а просто выполнить следующие действия:
- добавить временную форму сигнала в эксперимент с помощью функции SetSignal()
- добавить границу областей TFSF с помощью функций AddTFSFPlane() или AddTFSFBox()
- добавить плоскую TFSF волну с помощью функции SetPlaneWave() и/или точечные источники TFSF с помощью функции AddTFSFDipole()
Пример задания границы областей TF/SF плоскостью и запуска плоской волны:
#include "uiexp.h" int main(int argc,char **argv){ emInit(argc,argv); // инициализируем библиотеку EMTL uiExperiment task; // создание эксперимента task.SetInternalSpace(Vector_3(-10,-10,-10), Vector_3(10,10,10)); // установим размеры task.SetResolution(1,0.5); // установим разрешение и фактор Куранта task.SetBC(BC_PER,BC_PER,BC_PML); // установим граничные условия для сторон счетной области ... // задать параметры среды, создать и добавить в эксперимент нужные геометрические тела // как это сделать подробно было описано выше task.AddTFSFPlane(INF,INF,-7); // установить плоскость, по которой будет проходить граница // областей TF/SF. Где будет какая область зависит от TF/SF источников // здесь плоскость не пересекает оси X и Y и пересекает ось Z в точке -7 // таким образом, эта плоскость параллельна плоскости XY task.SetPlaneWave(Vector_3(0,0,1),Vector_3(1,0,0)); // задать плоскую волну с направлением, заданным // вектором {0,0,1} и поляризованную в направлении // {1,0,0} (в плоскости XZ) task.AddVTKDetectorSet("vtk",Vector_3(-9,-9,-9),Vector_3(9,9,9),18); // добавить VTK детектор // подробнее про детекторы см.ниже task.BuildGeometry(); // построить геометрию эксперимента task.CalculateN(100); // выполнить 100 временных итераций task.Analyze(); // преобразовать накопленные данные с детекторов в выходные файлы return 0 }
–пример установки границы TFSF в виде box и установка точечных источников внутри этого box
–пример установки границы TFSF в виде box и установка точечный источников снаружи этого box
Внутренние источники тока.
Внутренние источники тока работают за счет модификации в уравнениях Максвелла для ячеек, на которых они расположены.
По умолчанию каждый добавленный в эксперимент внутренний источник тока добавляется в набор внутренних источников тока по умолчанию. Можно создать несколько наборов, например для того, чтобы каждому из них назначить свою временнУю форму сигнала.
Внутренние источники точка могут быть двух типов:
- Проволочный диполь (существуют два ограничения:
одинаковый для каждой точки проволочки в каждый момент времени, проволочка может быть только прямой);
- Точечный диполь (аналог проволочного диполя, характерные размеры которого много меньше шага сетки).
–пример проволочка с периодическими условиями границ на ее концах, чтобы расходилась цилиндрическая волна
–пример несколько точечных источников
–пример сравнение точечного источника и точечного источника TFSF
Создание собственной временной формы сигнала
У к TFSF диполю есть требования к реализации временного сигнала () по умолчанию der не определены. Должны быть правильно заданы der(-1) и der(-2).
–пример как создать собственную временную форму сигнала (какого кстати? просто взять беренгера?)
Детекторы
Для того, чтобы измерять поля внутри вычислительного объема, нужны детекторы. Они считывают значения полей в тех точках, куда они помещены, никак при этом на них не влияя. Значения на детекторах получаются путем интерполяции по близлежащим узлам сетки. В ходе численного эксперимента детекторы записывают свои показания в двоичные файлы. По окончанию расчетов, при запуске функции Analyse(), на основании этих двоичных файлов создаются читаемые текстовые файлы.
в EMTL существуют различные виды детекторов которые можно разделить на две группы: универсальные и специальные детекторы. При этом в EMTL принято оперировать не отдельными детекторами, а наборами детекторов.
К универсальным детекторам относятся:
- универсальный детектор, который записывает историю сигнала в виде таблицы с колонками t, x, y, z, Ex, Ey, Ez, Hx, Hy, Hz для времени, координат и значений полей E и H. На основании его данных можно например строить графики с помощью программы gnuplot.
- специальный детектор, который создает входные файлы с временем, координатами и значениями полей E и H для построения графиков и 3d представления в программе ParaView.
Добавить набор из универсальных детекторов можно с помощью функции AddDetectorSet(), а набор из специальных детекторов для ParaView функцией AddVTKDetectorSet(). При этом необходимо указать два противоположных угла сетки детекторов и количество детекторов по осям. Если нужен только один детектор, можно создать сетку детекторов с размерностью по осям =1 и координатами противоположных углов, равными необходимым координатам создаваемого детектора.
Для универсальных детекторов также можно указать следующие конфигурационные флаги (можно указать несколько, разделив их символом '|'):
- DET_POINT (установлен по умолчанию) - создавать отдельный файл для каждого детектора в этом наборе детекторов
- DET_TSTEP - создавать отдельный файл для каждого временного шага, но с показаниями сразу всех детекторов (это может быть полезно при создании анимаций)
- DET_MESH (установлен по умолчанию) - записываются данные, взятые с сетки полей E и H.
- DET_SRC - записывает аналитическую форму сигнала в точке, в которой находится детектор от набора источников по умолчанию или от набора, указанного в srcid.
- DET_F - к записываемым данным применяется частотное преобразование Фурье (только для точечных источников)
- DET_ONFLY - при этом, если применяется частотное преобразование Фурье, указывает, что его необходимо делать сразу во время расчета (после каждого временного шага).
Для специальных детекторов, предназначенных для использования в программе ParaView можно указать количество доменов, но которые необходимо разбивать выходные данные. По умолчанию этот параметр равен 1. Разбиение выходных данных на домены может пригодится при использовании ParaView сервера запущенного на кластере, который будет обрабатывать их параллельно.
–какие примеры сюда вставить?
К специальным детекторам относятся:
- NearToFar - применяется для преобразования полей из ближнего поля в дальнее
- RTA - применяется для измерения прохождения, отражения и поглощения сигнала от структуры
- Flux - применяется для измерения потоков энергии через поверхности